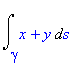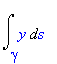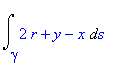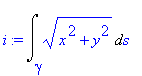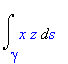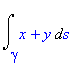Křivkový integrál I. druhu v systému Maple

Podpora pro výpočet tohoto integrálu je v rozšiřující knihovně student, která obsahuje příkaz Lineint. V tomto případě jde jen o matematický zápis křivkového integrálu. Další možností je užít příkaz PathInt z rozšiřující knihovny VectorCalculus. Předpokládejme, že hladká křivka je zadána parametricky x=x(t), y=y(t), z=z(t), a<=t<=b .

Syntaxe je

Lineint( integrand(x,y,z), x=x(t),y=y(t),z=z(t),t=a..b ) ... student package
PathInt( integrand(x,y,z), [x,y,z] = křivka ) ... VectorCalculus package

Ještě připomeňme, že systém Maple rozlišuje velká a malá písmena, protože pro výpočet křivkového integrálu II. druhu se používá podobný příkaz (LineInt).

> restart:
> with(student):
> Int(F(x,y,z),s=gamma..``)=
Lineint(F(x,y,z),x,y,z,t=a..b);

První příkaz vynuluje všechny dosavadní výsledky, druhý nahraje rozšiřující knihovnu do paměti

Druhá možnost výpočtu, pomocí PathInt, bude uvedena až přímo u jednotlivých příkladů, protože obecný zápis je spíše matoucí.

Nyní uveďme několik příkladů na výpočet tohoto druhu integrálu. Aplikace křivkového integrálu I. druhu naleznete v příkladech 7-13. Z důvodu délky dokumentu nejsou ve výčtu řešených příkladů zobrazeny obrázky. Kompletní řešení najdete u každého příkladu pomocí odkazu na řešení.

Řešené příklady

Příklad 1

Spočtěte následující křivkový integrál po po částech hladké křivce, která je zadána třemi vrcholy trojúhelníka.

Řešení příkladu

Příklad 2

Spočtěte křivkový integrál přes úsek paraboly y^2=2

x vymezený průsečíky s parabolou x^2=2

Řešení příkladu

Příklad 3

Spočtěte křivkový integrál podél křivky x^2+y^2=r*y , jde o kružnici .

Řešení příkladu

Příklad 4

Spočtěte křivkový integrál po oblouku evolventy kružnice

Řešení příkladu

Příklad 5

Spočtěte křivkový integrál po druhém závitu pravotočivé šroubovice

Řešení příkladu

Příklad 6

Spočtěme následující integrál po křivce, která je průnikem koule a roviny x=y .

Řešení příkladu

Na dalších příkladech ukážeme využití křivkového integrálu I. druhu v praxi a to při výpočtu délky křivky, těžiště křivky, hmotnosti křivky popř. plošného obsahu.

Příklad 7

Vypočtěte délku oblouku cykloidy.

Řešení příkladu

Příklad 8

Spočtěte délku kardioidy.

Řešení příkladu

Příklad 9

Spočtěte hmotnost části elipsy v I. kvadrantu, je-li délková hustota v každém bodě elipsy rovna y -ové souřadnici daného bodu.

Řešení příkladu

Příklad 10

Vypočtěte těžiště části asteroidy v I. kvadrantu

Řešení příkladu

Příklad 11

Určete statický moment 1. závitu kuželové šroubovice vzhledem k souřadnicové rovině xy , je-li délková hustota v každém bodě křivky rovna kvadrátu vzdálenosti od roviny xy .

Řešení příkladu

Příklad 12

Vypočtěte plošný obsah části válcové plochy x^2+y^2=r^2 omezené rovinnou z=0 , a plochou z=r-x^2/r .

Řešení příkladu

Příklad 13

Nalezněte těžiště 1. závitu šroubovice

Řešení příkladu

Ing. Vladimír Žák

MAPLE

Matematika

Knihovny

Informace

Řešené příklady