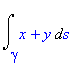
Příklad 6

Spočtěme následující integrál po křivce, která je průnikem koule a roviny x=y .

>	restart:with(student):with(plots):with(VectorCalculus):

Warning, the name changecoords has been redefined

Warning, the assigned names <,> and <|> now have a global binding

Warning, these protected names have been redefined and unprotected: *, +, ., Vector, diff, int, limit, series

>	Int(x+y,s=gamma..``);

Rovnice křivky

>	x^2+y^2+z^2=r^2;x=y;r>0;

Nejprve nakresleme obrázek, pro který je nutné zvolit pevné r , v našem případě pro jednoduchost r=1

>	p:=implicitplot3d(x^2+y^2+z^2=1^2,x=0..2,y=0..2,z=0..2, numpoints=5000,color=green,style=patchnogrid):

# Příkaz pro vykreslení funkce ve 3D, která je dána implicitně. Parametr numpoints  je nastaven na vyšší hodnotu, aby byla koule zobrazena jako koule. Parametrem patchnogrid  nebudeme zobrazovat triangulaci na dané ploše.

>	p1:=implicitplot3d(x-y,x=0..2,y=0..2,z=0..2, numpoints=5000,color=yellow,style=patchnogrid):

# Pro lepší zobrazení průniku obou ploch zobrazíme křivku, a to pomocí jejího parametrického vyjádření, které odvodíme později.

>	p2:=spacecurve([sqrt(2)/2*sin(t),sqrt(2)/2*sin(t),cos(t)], t=0..Pi/2,color=red,thickness=8,numpoints=5000, style=patchnogrid):

# Následujícím příkazem vykreslíme předchozí grafy do jedno hoobrázku a pomocí parametru orientation  určíme výchozí pohled.

>	display({p,p1,p2},orientation=[-24,63]);

Zavedeme parametrizaci této křivky ( zvolíme nejprve z  a pak dosadíme do rovnice koule).

>	par:=x=sqrt(2)/2*r*sin(t),y=sqrt(2)/2*r*sin(t), z=r*cos(t),t=0..Pi/2;

Počítáme tedy integrál

>	i:=Lineint(x+y,par);

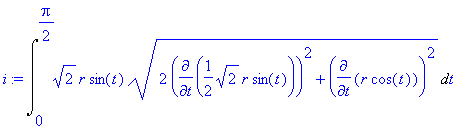
>	assume(r>0);

# Podmínka  na r

Výsledek je po

>

value(i);

Výpočet pomocí PathInt .

>	PathInt(x+y,[x,y,z] = Path(<sqrt(2)/2*r*sin(t), sqrt(2)/2*r*sin(t),r*cos(t)>,t=0..Pi/2));

>

>