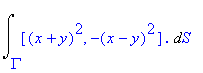| Křivkový integrál II. druhu v systému Maple | |
|
Úvodní slovo Autor MAPLESystém MapleZáklady práce Konstrukce Maple Definice funkcí Zjednodušování Řešení rovnic Grafické zpracování Programování MatematikaDiferenciální početIntegrální počet Křivkový integrál
Knihovnyplotsstudent Student VectorCalculus InformaceDownloadOdkazy Publikace |
Systém Maple obsahuje pro výpočet křivkového integrálu II. druhu příkaz LineInt z rozšiřující knihovny VectorCalculus.
Syntaxe: LineInt(F, dom) , kde F je vektorové pole určené danou soustavou souřadnic, dom je jednou z následujících konstrukcí, pomocí kterých definujeme křivku (např. Path, Circle, Ellipse, LineSegments ...). Následují řešené příklady na výpočet křivkového integrálu II. druhu. Všimněte si zejména posledního příkladu, tj. příkladu 5, neboť tento příklad obsahuje všechny možné postupy výpočtu křivkového integrálu II. druhu. Řešené příkladyPříklad 1Vypočtěte křivkový integrál druhého druhu
Příklad 2 Spočtěte zadaný křivkový integrál podél kladně orientovaného obvodu trojúhelníku určeného souřadnicovými osami a přímkou
Příklad 3 Spočtěte následující integrál podél prvního oblouku cykloidy
A to pomocí skalárního součinu a dále pomocí knihovny VectorCalculus.
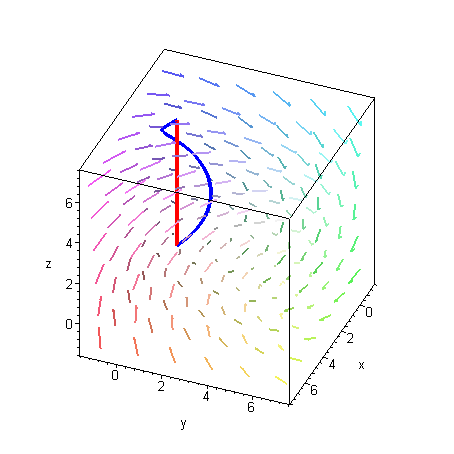
Příklad 4 Spočtěte křivkový integrál podél sjednocení dvou křivek
Příklad 5 Následující příklad postupně spočítáme čtyřmi postupy: pomocí skalárního součinu, pomocí VectorCalculus , užitím Greenova vzorce, pomocí potenciálu.
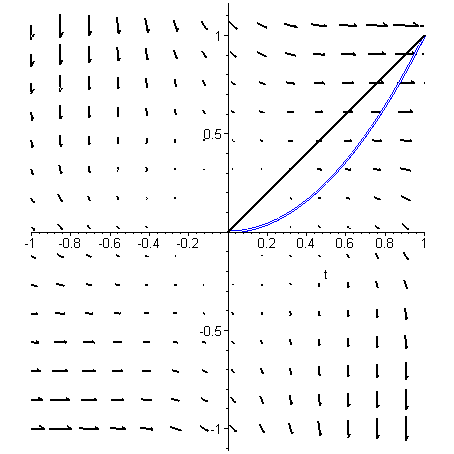
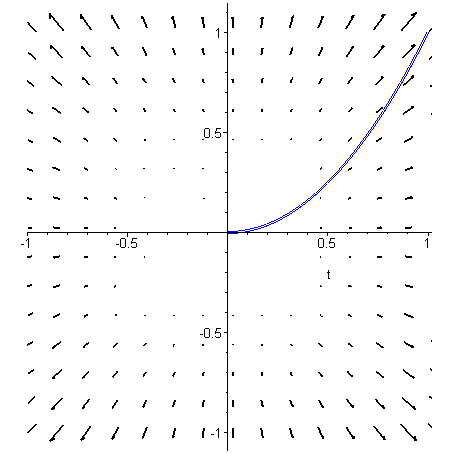
Příklad 6 Tento příklad slouží k výpočtu křivkového integrálu s využitím potenciálu. Vypočtěte křivkový integrál podél části paraboly dané body [0,0], [1,1]
|
| Ing. Vladimír Žák | |
![[Maple Plot]](image/krint_2_pr110.gif)
![[Maple Plot]](image/krint_2_pr25.gif)
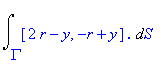
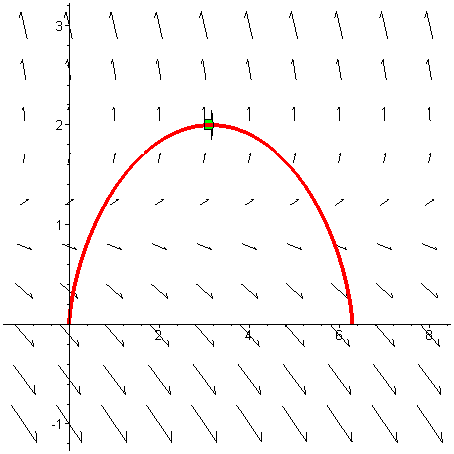
![Int([y, z, x]*`.`,S = Gamma .. ``)](image/krint_2_pr41.gif)