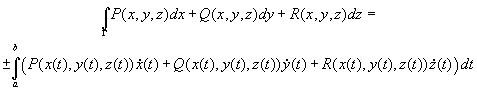| Křivkový integrál v systému Maple | |
|
Úvodní slovo Autor MAPLESystém MapleZáklady práce Konstrukce Maple Definice funkcí Zjednodušování Řešení rovnic Grafické zpracování Programování MatematikaDiferenciální početIntegrální počet Křivkový integrál Plošný integrál Knihovnyplotsstudent Student VectorCalculus InformaceDownloadOdkazy Publikace |
Pojem křivkového integrálu stejně jako pojem plošného integrálu probíraného v následující kapitole je nedílnou součástí integrálního počtu funkcí více proměnných. Systém Maple obsahuje několik příkazů, které dovedou v některých případech tyto integrály spočítat. Nejprve připomeňme, že se křivkové integrály dělí stejně jako plošné na dva druhy.
Přesné definice těchto integrálů lze najít např. ve skriptech: Ženíšek A. : Křivkový a plošný integrál, PC-DIR Real, s.r.o. Brno, 1999. Práce s křivkovými intehrály v systému Maple je také rozdělena na dvě části, a to na: Následuje definice plošného integrálu, ať už prvního a nebo druhého druhu. Plošný integrál I. druhuPodpora pro výpočet tohoto integrálu je v rozšiřující knihovně student , která obsahuje příkaz Lineint . V tomto případě jde jen o matematický zápis křivkového integrálu. Další možností je užít příkaz PathInt z rozšiřující knihovny VectorCalculus . Předpokládejme, že hladká křivka je zadána parametricky x=x(t) , y=y(t) , z=z(t) , a<=t<=b . Pak křivkový integrál můžeme zapsat:
Křivkový integrál I. druhu v systému Maple Plošný integrál II. druhuKřivkový integrál II. druhu můžeme pro orientovanou křivku danou parametrickými rovnicemi
Tento integrál lze také vyjádřit pomocí skalárního součinu
Křivkový integrál II. druhu v systému Maple |
| Ing. Vladimír Žák | |