Pro vytváření vlastních procedur v systému Maple je vytvořen speciální jazyk. Tato kapitola není úplným referenčním textem, je jen základem pro pochopení struktur vlastních procedur. Při programování se velmi často používají cykly a podmínky, a proto i systém Maple tyto řídící struktury obsahuje.

Zopakujme syntaxi pro vytvoření vlastní funkce (procedury). Struktura vypadá následovně

název_fce := proc(param1,param2,…)
         tělo funkce
end proc;

Nejprve zvolíme název funkce a pak pomocí klíčového slova proc vytvoříme funkci s parametry, které jsou uzavřeny do kulatých závorek. Dále následuje tělo funkce , ve kterém se většinou vyhodnotí zadané parametry a jejich typy, provedou se příslušné příkazy a konstrukce se ukončí pomocí end proc .

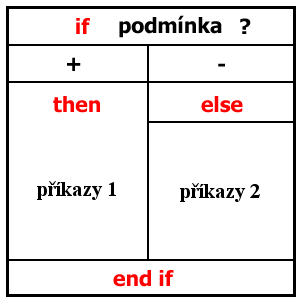
Nyní se podívejme na řízení toku programu pomocí struktury (podmínky)
     if-then-else-end if .
Přesná syntaxe je

if podmínka1 then příkazy1 else příkazy2 end if

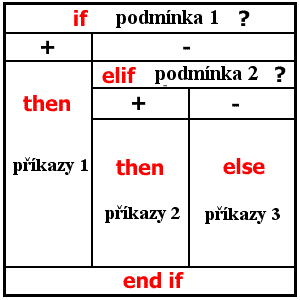
Je-li podmínka za if splněna (tj. + ), jsou provedeny příkazy uvedené za then . Pokud splněna není ( tj. - ), provedou se příkazy uvedené za else . V obou případech se hned po provedení příkazů pokračuje v programu.

Existuje ještě jiná možnost zápisu podmínky s if , a to

if podmínka1 then příkazy1 elif podmínka2 then příkazy2 else příkazy3 end if

Následující obrázek ukazuje, jak tato struktura pracuje.

Nyní si na příkladu hledání maxima ze dvou zadaných čísel ukažme použití těchto dvou struktur. Z pedagogických důvodů budeme požadovat i informaci o případné rovnosti čísel. Příklad později rozšíříme na hledání maxima z libovolného počtu zadaných čísel, a to pomocí cyklů typu for-do nebo while-do.

Výše uvedenou proceduru lze samozřejmě zapsat i bez použití else , ale jako ukázka je vhodnější výše uvedený kód. Nyní s výhodou užijeme struktury s elif .

V předchozím zdrojovém kódu si hlavně všimněte předposledního řádku, kde je uvedena alternativa ukončení k end if , tj. fi .

Nyní přistupme k dalším strukturám, půjde o cykly.

Začneme s cyklem while-do-end do . Přesnější syntaxe je

     while podmínka do příkazy end do

Jde o cyklus s podmínkou, je-li pravdivá, jsou provedeny příkazy za klíčovým slovem do . Následující obrázek ukazuje, jak tento cyklus pracuje.

Vraťme se k proceduře hledání maxima. Nyní ji změníme pro libovolný počet zadaných parametrů s využitím cyklu while-do .

> max3:=proc()      # podmínka while-do-end do
   local i,n,max;   # definice lokálních proměnných
    n:=nargs;
      # počet vložených parametrů do fce max3
    max:=args[1];
      # jako maximum nastavíme 1. parametr
    i:=2;
      # začneme porovnávat až od druhého parametru
    while i<=n do
      if args[i]>max then
        max:=args[i];
        # je-li parametr větší než max, přepíšeme max
      end if;
      i:=i+1;
      # přejdeme k následujícímu parametru
    end do;
    return max;     # vypíšeme maximum
end proc:

Přistupme k vysvětlení předchozí procedury. Pokud potřebujeme nějaké vlastní (lokální) proměnné, které budou pouze v těle procedury, je nutné užít klíčového slova local. V případě, že tyto proměnné nejsou takto předem deklarovány, Maple ohlásí varování.
    Podíváme-li se znovu na předchozí zdrojový kód, zjistíme, že nejsou zadány žádné parametry. To je ale omyl. Procedura počítá minimálně s jedním, a to při inicializaci proměnné max. K zadaným parametrům se v Maplu přistupuje pomocí pole args[i] a celkový počet zadaných parametrů je obsažen v nargs.
    Vraťme se k předchozímu kódu. Dále následuje inicializace maxima prvním zadaným parametrem a pak pomocí cyklu while-do procházíme a porovnáváme zbylé parametry s hodnotou uloženou v max . Nakonec je maximum vypsáno.

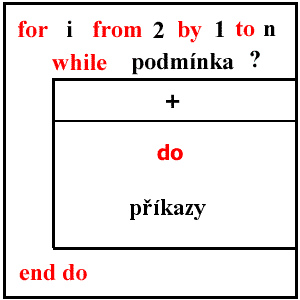
Pokud znáte jiný programovací jazyk, např. jazyk C, pravděpodobně byste v tomto případě použili jiný cyklus a to cyklus for . I zde je to možné, protože i Maple nabízí tento často užívaný cyklus. Podívejme se blíže na jeho dvě možné syntaxe.

for proměnná from odkud by krok to kam while podmínka do příkazy end do

nebo

for proměnná in struktura while podmínka do příkazy end do

V prvním příkazu se proměnná inicializuje hodnotou uvedenou za klíčovým slovem from , zvyšovat se bude o hodnotu kroku dokud nedosáhne hodnoty kam . Dále se vyhodnotí podmínka příkazu while a pokud je splněna, jsou provedeny příkazy . Následující obrázek vše vysvětlí lépe.

Ukažme si to na dalším možném zápisu naší známé procedury hledání maxima.

> max4:=proc()
   local i,max;
       # definice lokálních proměnných
   max:=args[1];
       # jako maximum nastavíme 1. parametr
   for i from 2 to nargs do
       # začneme porovnávat až od druhého parametru
     if args[i]>max then
       # je-li parametr větší než max, přepíšeme max
       max:=args[i];
     end if;
   end do;
   return max;
       # vypíšeme maximum
   end proc:

Volání funkce.

> max4(5,-6);

> max4();
# procedura zde hlásí chybu, protože
# se snaží přistupovat k prvnímu prvku pole
# argumentů, ale tento prvek neexistuje

Error, (in max4) invalid subscript selector

> max4(0,-65,76);

> max4(0,-6,76,-98.25,78,78);

Nyní se podívejme na cyklus for-in-do . Mějme seznam čísel, které chceme postupně sčítat, dokud nedosáhneme určité hodnoty.

> cisla:=[1,4,6,7,12,15,20]: mmax:=0:
> for z in cisla while mmax<=30 do
    mmax:=mmax+z; end do:

> mmax;

Výše uvedený zdrojový kód je snáze čitelný. Všimněme si, že místo proměnné max je užita proměnná mmax , a to proto, že max je klíčovým slovem systému Maple. V předchozích zdrojových kódech mohla být proměnná max používána bez nebezpečí, protože byla deklarována jako lokální, pomocí local .