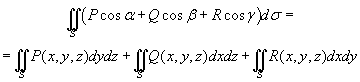Pojem plošného integrálu stejně jako pojem křivkového integrálu probíraného v předchozí kapitole je nedílnou součástí integrálního počtu funkcí více proměnných. Systém Maple obsahuje několik příkazů, které dovedou v některých případech tyto integrály spočítat. Nejprve připomeňme, že se plošné integrály dělí stejně jako křivkové na dva druhy.

Přesné definice těchto integrálů lze najít např. ve skriptech:
Ženíšek A. : Křivkový a plošný integrál, PC-DIR Real, s.r.o. Brno, 1999.

Práce s plošnými intehrály v systému Maple je také rozdělena na dvě části, a to na:

• Plošný integrál I. druhu v systému Maple
• Plošný integrál II. druhu v systému Maple

Následuje definice plošného integrálu, ať už prvního a nebo druhého druhu.

Plošný integrál I. druhu

Pro připomenutí uvedeme pouze zápis tohoto druhu integrálu v případě silné regularity úseku S vzhledem k xy daného rovnicí z=f(x,y).

Předpokladem pro tento zápis je silná regularita úseku plochy S vzhledem k xy, dále spojitost funkce F na S a spojitost funkce f(x,y) a příslušných derivací. V případě, že úsek je zadán parametrickými rovnicemi, potom

Přesné definice naleznete např. výše uvedených skriptech.

Plošný integrál I. druhu v systému Maple.

Plošný integrál II. druhu

Základem je vektorové pole ve tvaru
> F(x,y,z)=(P(x,y,z),Q(x,y,z),R(x,y,z));

a normála ve tvaru
> n=(cos(alpha),cos(beta),cos(gamma));

Pak můžeme tento integrál zapsat

kde je regulární ke všem třem souřadnicovým rovinám, n(x,y,z) je jeho orientovaná jednotková normála a P,Q,R jsou funkce spojité na .

Přesné definice naleznete např. výše uvedených skriptech.

Plošný integrál II. druhu v systému Maple.