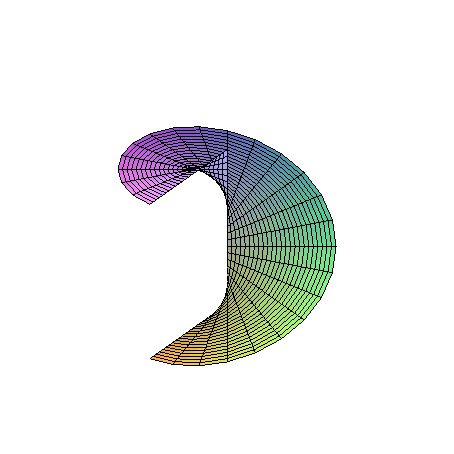| Plošný integrál I. druhu v systému Maple | |
|
Úvodní slovo Autor MAPLESystém MapleZáklady práce Konstrukce Maple Definice funkcí Zjednodušování Řešení rovnic Grafické zpracování Programování MatematikaDiferenciální početIntegrální počet Křivkový integrál Plošný integrál
Knihovnyplotsstudent Student VectorCalculus InformaceDownloadOdkazy Publikace |
Systém Maple obsahuje pro výpočet plošného integrálu I. druhu příkaz SurfaceInt , který je součástí rozšiřující knihovny VectorCalculus .
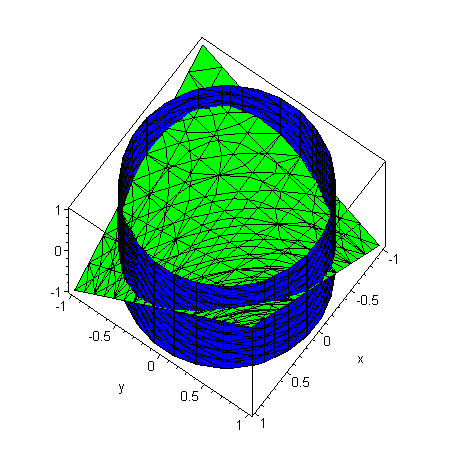
Více o použití těchto konstrukcí naleznete v kapitole o knihovně VectorCalculus nebo v následujících příkladech, popř.v nápovědě. Řešené příkladyPříklad 1Vypočtěte plošný integrál po části ležící v I. oktantu hyperbolického paraboloidu ohraničeného válcem.
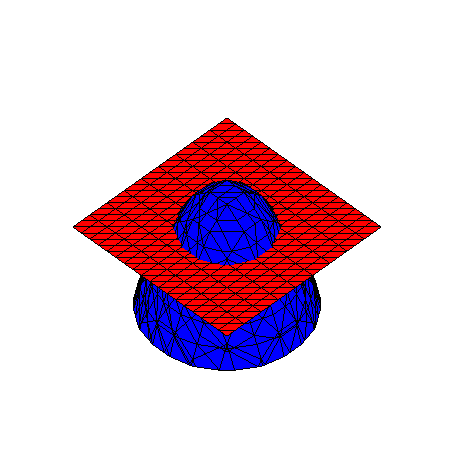
Příklad 2 Vypočtěte plošný integrál po části roviny z=1-x-y ležící v prvním oktantu.
Příklad 3 Spočtěte plošný obsah rotačního paraboloidu omezeného rovinou z=0 .
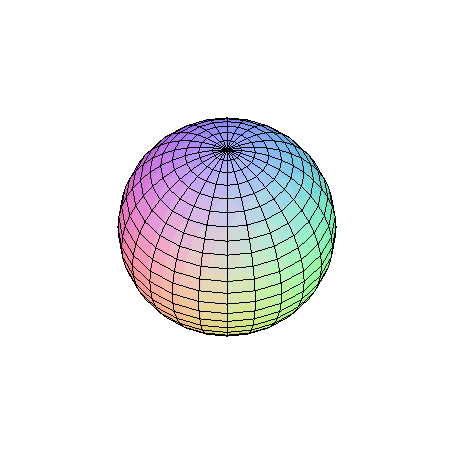
Příklad 4 Následující příklad ukazuje výpočet plošného integrálu pomocí jeho parametrického vyjádření . Určete hmotnost kulové plochy, je-li plošná hustota v každém bodě dané plochy rovna vzdálenosti bodu od osy z . Rovnice kulové plochy (není regulární) Plošná hustota
Příklad 5 Určete plošný obsah závitu šroubové konoidy
|
| Ing. Vladimír Žák | |