Příklad 3

Spočtěte plošný obsah rotačního paraboloidu omezeného rovinou z=0 .

>    restart:with(plots):with(student):with(VectorCalculus): 

Warning, the name changecoords has been redefined



Warning, the assigned names <,> and <|> now have a global binding



Warning, these protected names have been redefined and unprotected: *, +, ., Vector, diff, int, limit, series

Obsah plochy se vypočte pomocí následujícího integrálu [Maple OLE 2.0 Object]

Rovnice rotačního paraboloidu

>    rp:=z=r^2-x^2-y^2;

rp := z = r^2-x^2-y^2

Nakreslíme obrázek

>    p:=implicitplot3d(subs(r=1,rp),x=-2..2,y=-2..2,z=-2..2,
color=blue):

#  Pevně jsme zvolili r=1 .

>    p1:=implicitplot3d(z,x=-2..2,y=-2..2,z=-2..2,color=red):

#  Nakreslení roviny.

>    display({p,p1});

[Maple Plot]

Vypočítáme příslušné derivace

>    f:=r^2-x^2-y^2;

f := r^2-x^2-y^2

>    fx:=diff(f,x);

fx := -2*x

>    fy:=diff(f,y);

fy := -2*y

Dosadíme do integrálu, který budeme počítat přes průmět plochy do souřadnicové roviny xy  - jde o kruh.

>    i:=Doubleint(1*sqrt(1+fx^2+fy^2),x,y,S[xy]);

i := Int(Int((4*x^2+1+4*y^2)^(1/2),x = S[xy] .. ``),y = `` .. ``)

Zavedeme polární souřadnice

>    assume(u>0);

>    changevar({x=u*cos(v),y=u*sin(v)},subs(S[xy]=S[uv],i),[u,v]);

Int(Int((1+4*u^2)^(1/2)*u,u = S[uv] .. ``),v = `` .. ``)

#  Systém Maple neumí transformovat meze integrace!

Integrujeme přes kruh, počítáme tedy integrál

>    Doubleint(integrand(%),u=0..r,v=0..2*Pi);

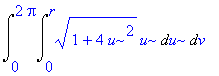
Int(Int((1+4*u^2)^(1/2)*u,u = 0 .. r),v = 0 .. 2*Pi)

Výsledkem je

>    value(%);

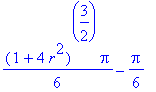
1/6*(1+4*r^2)^(3/2)*Pi-1/6*Pi

Systém Maple nabízí rychlejší řešení s využitím příkazu SurfaceInt .

>    SurfaceInt(1,[x,y,z] = Surface(<s,t,r^2-s^2-t^2>,[s,t]=
Circle(<0,0>,r)));

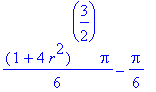
1/6*(1+4*r^2)^(3/2)*Pi-1/6*Pi

#  Využili jsme konstrukce Circle , která popíše kruh pomocí středu a poloměru.

>   

TOPlist