Příklad 1

Vypočtěte plošný integrál    po části ležící v I. oktantu hyperbolického paraboloidu ohraničeného válcem.

>	restart:with(student):with(plots):with(VectorCalculus):

Warning, the name changecoords has been redefined

Warning, the assigned names <,> and <|> now have a global binding

Warning, these protected names have been redefined and unprotected: *, +, ., Vector, diff, int, limit, series

Rovnice paraboloidu

>

z=x*y;

Rovnice válce

>	val:=x^2+y^2=r^2;

Nakreslíme obrázek

>	p:=implicitplot3d(z=x*y,x=-1..1,y=-1..1,z=-1..1, color=green):

>	p1:=implicitplot3d(x^2+y^2=1,x=-1..1,y=-1..1,z=-1..1, color=blue):

#  Vykreslení funkce dané implicitně ve 3D.

>	display({p,p1},orientation=[36,22],axes=boxed);

Oblast je silně regulární vzhledem k xy , tedy můžeme použít vzorec , kde funkce z=f(x,y)=x*y .

Zapíšeme funkci f(x,y)  a spočteme příslušné derivace.

>

f:=x*y;

>	fx:=diff(f,x);

>	fy:=diff(f,y);

Po dosazení dostáváme dvojný integrál přes průmět plochy S  do roviny xy , tj. přes čtvrtkruh.

>	i:=Doubleint(f*sqrt(x^2+y^2+1)*sqrt(1+fx^2+fy^2),x,y,S[xy]);

Zavedeme polární souřadnice

>	assume(u>0);

>	changevar({x=u*cos(v),y=u*sin(v)},subs(S[xy]=S[uv],i),[u,v]);

#  Příkaz changevar  neumí transformovat meze integrálu, proto nebyly v předchozím příkazu uvedeny a bylo použito jiného označení pro oblast integrace.

Integrujeme přes čtvrtkruh, počítáme tedy

>	Doubleint(integrand(%),u=0..r,v=0..Pi/2);

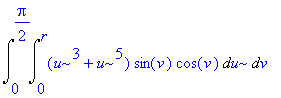
#  Pomocí příkazu   integrand  získáme integrand z předchozího integrálu.

Vypočteme integrál

>

value(%);

Pro zrychlení výpočtů lze užít příkazy z VectorCalculus .

>	assume(r>0);

>	SurfaceInt( z*(x^2+y^2+1)^(1/2),[x,y,z]=Surface( <s,t,s*t>, s=0..r, t=0..sqrt(r^2-s^2)));

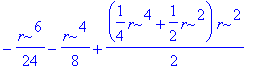
>	simplify(%);

#  Příkaz Surface  určí plochu, přes kterou se bude integrovat. Využilo se rovnice válce.