Příklad 5

Určete plošný obsah závitu šroubové konoidy

>    restart:with(student):with(plots):
with(VectorCalculus):with(linalg): 

Warning, the name changecoords has been redefined



Warning, the assigned names <,> and <|> now have a global binding



Warning, these protected names have been redefined and unprotected: *, +, ., Vector, diff, int, limit, series



Warning, the previous binding of the name Wronskian has been removed and it now has an assigned value



Warning, the protected names norm and trace have been redefined and unprotected

Parametrické rovnice konoidy

>    X:=u*cos(v);
Y:=u*sin(v);
Z:=v;

X := u*cos(v)

Y := u*sin(v)

Z := v

Rozsahy parametrů

>    ru:=u=0..r;
rv:=v=0..2*Pi;

ru := u = 0 .. r

rv := v = 0 .. 2*Pi

Nakreslíme obrázek pro pevně zvolené r=1

>    plot3d([X,Y,Z],u=0..1,rv);

[Maple Plot]

Výpočet integrálu pomocí jeho parametrického vyjádření.

Určíme normálu

>    n:=[A,B,C]:

>    M:=Matrix([diff([X,Y,Z],u),diff([X,Y,Z],v)]);

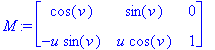
M := Matrix(%id = 2774720)

#  Matice derivací jednotlivých funkcí X , Y , Z .

>    submatrix(M,1..2,2..3);
A:=det(%);

matrix([[sin(v), 0], [u*cos(v), 1]])

A := sin(v)

#  Výpočet determinantu submatice, která charakterizuje A .  

>    submatrix(M,[1,2],[1,3]);
B:=det(%);

matrix([[cos(v), 0], [-u*sin(v), 1]])

B := cos(v)

#  Druhá složka normály

>    submatrix(M,1..2,1..2);
C:=simplify(det(%));

matrix([[cos(v), sin(v)], [-u*sin(v), u*cos(v)]])

C := u

#  Třetí složka normály

>    n;

[sin(v), cos(v), u]

Nyní určíme velikost normály

>    H:=sqrt(A^2+B^2+C^2);

H := (cos(v)^2+sin(v)^2+u^2)^(1/2)

Zjednodušíme pomocí známého vzorce

>    simplify(H,{sin(v)^2+cos(v)^2=1});

(1+u^2)^(1/2)

Počítáme integrál

>    Doubleint(%,sigma,``,S);

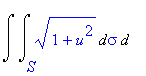
Int(Int((1+u^2)^(1/2),sigma = S .. ``),`` = `` .. ``)

Po dosazení obdržíme

>    Doubleint(integrand(%),ru,rv);

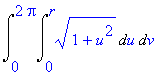
Int(Int((1+u^2)^(1/2),u = 0 .. r),v = 0 .. 2*Pi)

Výsledek vypočteme pomocí

>    value(%);

r*(1+r^2)^(1/2)*Pi+arcsinh(r)*Pi

>    convert(%,ln);

r*(1+r^2)^(1/2)*Pi+ln(r+(1+r^2)^(1/2))*Pi

#  Při tradičním výpočtu dostáváme tento výsledek. Pomocí předchozího příkazu můžeme výsledek vypočtený systémem Maple převést na požadovaný tvar.

Výpočet pomocí knihovny VectorCalculus

>    SurfaceInt(1,[x,y,z]=Surface(<X,Y,Z>,ru,rv));

Pi*(r*(1+r^2)^(1/2)+arcsinh(r))

>   

TOPlist