Příklad 4

Následující příklad ukazuje výpočet plošného integrálu pomocí jeho parametrického vyjádření .

>	restart:with(student):with(plots): with(VectorCalculus):with(linalg):

Warning, the name changecoords has been redefined

Warning, the assigned names <,> and <|> now have a global binding

Warning, these protected names have been redefined and unprotected: *, +, ., Vector, diff, int, limit, series

Warning, the previous binding of the name Wronskian has been removed and it now has an assigned value

Warning, the protected names norm and trace have been redefined and unprotected

Určete hmotnost kulové plochy, je-li plošná hustota v každém bodě dané plochy rovna vzdálenosti bodu od osy z .

Rovnice kulové plochy (není regulární)

>	kp:=x^2+y^2+z^2=r^2;

Plošná hustota

>	mu:=sqrt(x^2+y^2);

Hmotnost plochy se spočítá pomocí  , kde  je plošná hustota.

Parametrické rovnice koule

>	X:=r*cos(u)*sin(v):

>	Y:=r*sin(u)*sin(v):

>	Z:=r*cos(v):

Pro kontrolu nakreslíme obrázek

>	plot3d([cos(u)*sin(v),sin(u)*sin(v),cos(v)],u=0..2*Pi, v=0..Pi);

Dále určíme normálu

>	n:=[A,B,C];

Jednotlivé složky určíme pomocí příkazů  z rozšiřující knihovny linalg . Nejprve určíme příslušné derivace.

>	N:=Matrix([diff([X,Y,Z],u),diff([X,Y,Z],v)]);

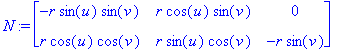
#  Matice derivací funkcí X , Y , Z .

>	submatrix(N,1..2,2..3); A:=det(%);

#  Výpočet determinantu submatice, která charakterizuje A .  

>	submatrix(N,[1,2],[1,3]); B:=det(%);

#  Druhá složka normály

>	submatrix(N,1..2,1..2); C:=simplify(det(%));

#  Třetí složka normály

Nyní určíme velikost normály

>	H:=sqrt(A^2+B^2+C^2);

Zjednodušíme pomocí známého vzorce

>	simplify(H,{sin(u)^2+cos(u)^2=1,sin(v)^2+cos(v)^2=1});

Využijeme tentýž vzorec

>	simplify(%,{1-cos(v)^2=sin(v)^2});

>	assume(r>0,sin(v)>0);

>	H:=simplify(%,{1-cos(v)^2=sin(v)^2});

#  Mohli jsme omezit sin  kvůli rozsahu v .

Dosazením do   dostaneme dvojný integrál

>	Doubleint(subs(x=X,y=Y,sqrt(x^2+y^2))*H,u,v,M);

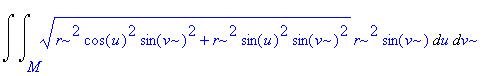
>	i:=Doubleint(integrand(%),u=0..2*Pi,v=0..Pi);

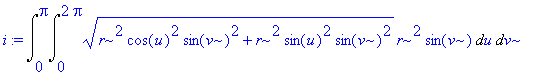
#  Získání integrandu a přidání integračních mezí.

>	simplify(i,{sin(u)^2+cos(u)^2=1,sin(v)^2+cos(v)^2=1});

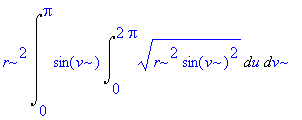
#  Zjednodušení známými rovnicemi.

>	simplify(%,{1-cos(v)^2=sin(v)^2});

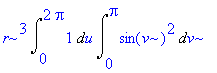
Výsledná hodnota je

>	simplify(value(%));

Nyní se podívejme na postup výpočtu pomocí příkazů z knihovny VectorCalculus .

>	SurfaceInt(mu,[x,y,z]=Sphere(<0,0,0>,r));

#  Prvním parametrem je plošná hustota. Plochu určíme přímo pomocí konstrukce Sphere .

>