Příklad 4

Spočtěte křivkový integrál podél sjednocení dvou křivek

>	restart:with(plots):

Warning, the name changecoords has been redefined

>	Int([y,z,x]*`.`,S=Gamma..``);

>	vpole:=[y,z,x];

# Vektorové pole

Parametrické rovnice šroubovice

>	par:=r*cos(t),r*sin(t),v*t,t=0..2*Pi; _par:=x=r*cos(t),y=r*sin(t),z=v*t,t=0..2*Pi;

Druhou křivkou je úsečka zadaná body

>	body:=[[r,0,0],[r,0,2*Pi*v]];

Nakreslíme obrázek pro pevně zvolené parametry, r=1 , v=r .

>	p:=fieldplot3d(vpole,x=-1..7,y=-1..7,z=-1..7,grid=[6,6,6],thickness=2):

# Vykreslení vektorového pole ve 3D.

>	p1:=spacecurve(subs(r=1,v=1,[par]),thickness=4,color=blue):

# Křivka v prostoru, proto příkaz spacecurve .

>	p2:=spacecurve(subs(r=1,v=1,body),thickness=4,color=red):

>	display({p,p1,p2},axes=boxed,orientation=[22,55]);

• výpočet pomocí skalárního součinu

Nejprve spočteme křivkový integrál podél šroubovice. Dosazením parametrických rovnic do integrandů dostáváme

>	parpole:=[subs(_par[1],_par[2],_par[3],vpole[1]),subs(_par[1],_par[2],_par[3],vpole[2]), subs(_par[1],_par[2],_par[3],vpole[3])];

#  Příkaz subs  provádí vícenásobnou substituci, tj. substituční rovnice musí být zadány jako posloupnost, poslední parametr určuje místo použití.

Přesný zápis integrálu se skalárním součinem tedy je

>	Int(parpole.Diff([par[1],par[2],par[3]],t), par[4]);

Nyní provedeme naznačenou derivaci

>	dpar:=diff([par[1],par[2],par[3]],t);

Počítáme tedy integrál

>	Int(parpole.dpar, par[4]);

Pro výpočet skalárního součinu užijeme příkazu dotprod  z knihovny linalg .

>	arg:=linalg[dotprod](parpole,dpar,'orthogonal');

# Integrand

Počítáme tedy integrál a výsledkem je

>	i:=Int(arg,par[4])=int(arg,par[4]);

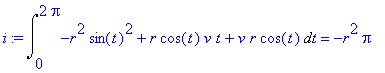
Dále  spočtěme integrál podél úsečky
Jednou z možných parametrizací úsečky je

>	_par1:=[x=r,y=0,z=2*Pi*v-2*Pi*v*t,t=0..1]; par1:=[r,0,2*Pi*v-2*Pi*v*t,t=0..1];

Dosazením parametrických rovnic do integrandů dostáváme

>	parpole1:=[subs(op(1..3,_par1),vpole[1]),subs(op(1..3,_par1),vpole[2]), subs(op(1..3,_par1),vpole[3])];

#  Příkaz subs  provádí vícenásobnou substituci, tj. substituční rovnice musí být zadány jako posloupnost, poslední parametr určuje místo použití.

Přesný zápis integrálu se skalárním součinem tedy je

>	Int(parpole1.Diff([op(1..3,par1)],t), par1[4]);

Nyní provedeme naznačenou derivaci

>	dpar1:=[op(1..3,diff(par1,t))];

Počítáme tedy integrál

>	Int(parpole1.dpar1, par1[4]);

>	arg1:=linalg[dotprod](parpole1,dpar1,'orthogonal');

# Výpočet  integrandu

Počítáme tedy integrál a výsledkem je

>	i1:=Int(arg1,par1[4])=int(arg1,par1[4]);

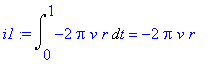
Výsledný integrál je roven součtu jednotlivých integrálů

>	rhs(i+i1);

• výpočet pomocí příkazu LineInt

>	with(VectorCalculus):

Warning, the assigned names <,> and <|> now have a global binding

Warning, these protected names have been redefined and unprotected: *, +, ., Vector, diff, int, limit, series

Nyní spočtěme jednotlivé integrály a výsledkem bude jejich součet.

>	LineInt(VectorField(<y,z,x>,cartesian[x,y,z]), Path(<r*cos(t),r*sin(t),v*t>,t=0..2*Pi));

# Po šroubovici.

>	LineInt(VectorField(<y,z,x>,cartesian[x,y,z]),Line(<r,0,2*Pi*v>,<r,0,0>));

# Po úsečce. Pozor jdeme z koncového bodu do počátečního!

Výsledkem je součet těchto integrálů

>

%+%%;

>