Příklad 5

Následující příklad postupně spočítáme čtyřmi postupy: pomocí skalárního součinu, pomocí VectorCalculus , užitím Greenova  vzorce, pomocí potenciálu.

>	restart:with(plots):

Warning, the name changecoords has been redefined

>	Int([(x+y)^2,-(x-y)^2]*`.`,S=Gamma..``);

Křivka je dána sjednocením části paraboly a úsečky zadané body  [0,0] , [1,1].

>	_par:=[x=t,y=t^2,t=0..1]; par:=[t,t^2,t=0..1];

# Parametrizace paraboly.

>	_par1:=[x=1-t,y=1-t,t=0..1]; par1:=[1-t,1-t,t=0..1];

# Parametrické rovnice úsečky.

>	vpole:=[(x+y)^2,-(x-y)^2];

# Zadání pole

Nakreslení obrázku

>	p:=plot(t^2,t=-1..1,color=WHITE): _p:=plot(t^2,t=0..1,color=blue,thickness=3):

# Graf části paraboly. První příkaz je v tomto tvaru, protože jinak by obrázek zahrnoval pouze interval <0,1> na ose x , což není vhodné kvůli lepší představě tvaru vektorového pole. Proto také byla zvolena křivka bílé barvy, protože splyne s pozadím..

>	p1:=polygonplot([[0,0],[1,1]],thickness=3):

# Vykreslení úsečky zadáním počátečního a koncového bodu.

>	p2:=fieldplot(vpole,x=-1..1.05,y=-1..1.05,grid=[15,15],thickness=2):

# Obrázek vektorového pole

>	display({p,_p,p1,p2},scaling=constrained);

• Výpočet pomocí skalárního součinu

Dosazením parametrických rovnic do integrandů obdržíme

>	parpole:=[subs(op(1..2,_par),vpole[1]),subs(op(1..2,_par),vpole[2])]; parpole1:=[subs(op(1..2,_par1),vpole[1]),subs(op(1..2,_par1),vpole[2])];

# Použili jsme příkaz op , jehož první parametr určuje počet prvků seznamu (popř. množiny) zadané ve druhém parametru, který bude vypsán jako posloupnost. Příkaz subs  provádí vícenásobnou substituci, tj. substituční rovnice musí být zadány jako posloupnost, poslední parametr určuje místo použití.

Přesný zápis integrálů se skalárním součinem  je

>	Int(parpole.Diff([par[1],par[2]],t), par[3]);

>	Int(parpole1.Diff([par1[1],par1[2]],t), par1[3]);

Nyní provedeme naznačenou derivaci

>	dpar:=[op(1..2,diff(par,t))]; dpar1:=[op(1..2,diff(par1,t))];

Počítáme tedy integrály

>	Int(parpole.dpar, par[3]);

>	Int(parpole1.dpar1, par[3]);

Jde o skalární součin dvou vektorů, proto použijeme příkaz dotprod  z rozšiřující knihovny linalg.

>	arg:=linalg[dotprod](parpole,dpar,'orthogonal');

>	arg1:=linalg[dotprod](parpole1,dpar1);

# Integrand

Počítáme tedy integrály

>	Int(arg,par[3])=int(arg,par[3]); Int(arg1,par1[3])=int(arg1,par1[3]);

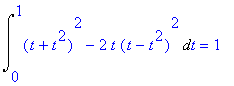
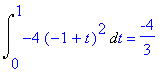
Výsledkem je jejich součet

>	rhs(%)+rhs(%%);

• Užitím knihovny VectorCalculus

>	with(VectorCalculus):

Warning, the assigned names <,> and <|> now have a global binding

Warning, these protected names have been redefined and unprotected: *, +, ., Vector, diff, int, limit, series

Vytvoříme vektorové pole v kartézské soustavě (z integrandů)

>	vf:=VectorField(<(x+y)^2,-(x-y)^2>,cartesian[x,y]);

>	i1:=LineInt(vf,Path(<t,t^2>,t=0..1));

# Výpočet po parabolu

>	i2:=LineInt(vf,Line(<1,1>,<0,0>));

# POZOR - křivka je orientována z koncového bodu do počátečního.

Výsledkem je součet jednotlivých integrálů

>

i1+i2;

• Užitím Greenova vzorce

Nejprve uveďme Greenův vzorec  . Předpokladem je normální oblast s po částech hladkou hranicí, dále spojitost P(x,y) , Q(x,y)  a jejich derivací, a kladná orientace hranice oblasti vzhledem k oblasti. Přesnou definici Greenovy věty lze nalézt např. v [1].

Z obrázku je patrné, že oblast ohraničená oběma křivkami je konvexní, tzn. je i normální. Orientace hranice vzhledem k oblasti je kladná (viz. obrázek).

>	with(student):

>	P:=(x+y)^2; Q:=-(x-y)^2;

# Určení funkcí P , Q  z původního integrálu

Provedeme naznačené derivace

>	dQ:=Diff(Q,x)=diff(Q,x); dP:=Diff(P,y)=diff(P,y);

Dosadíme do Greenova  vzorce

>	Doubleint(rhs(dQ)-rhs(dP),x,y,Omega);

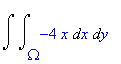
# Pomocí příkazu rhs  získáme pravou stranu rovnice.

Oblast  je omezena zdola parabolou a shora úsečkou. Podle obrázku lze snadno určit meze pro dvojný integrál.

>	Doubleint(rhs(dQ)-rhs(dP),y=x^2..x,x=0..1);

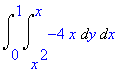
Spočteme hodnotu integrálu

>

value(%);

• Potenciál  (hledání kmenové funkce)

V kapitole o knihovně VectorCalculus  byl uveden příkaz pro výpočet potenciálu. Jde o příkaz ScalarPotential . Na tomto příkladu si ukážeme jeho použití. Ještě připomeňme, že výsledný integrál je roven rozdílu funkční hodnoty potenciálu v koncovém bodu a funkční hodnoty potenciálu v počátečním bodu. V tomto případě také mluvíme o nezávislosti křivkového integrálu na integrační cestě.

>	restart:with(VectorCalculus):

Warning, the assigned names <,> and <|> now have a global binding

Warning, these protected names have been redefined and unprotected: *, +, ., Vector, diff, int, limit, series

>	v:=VectorField(<(x+y)^2,-(x-y)^2>,cartesian[x,y]);

# Vektorové pole získané z integrandů

Výpočet potenciálu

>	ScalarPotential(v);

Je vidět, že potenciál neexistuje, což je v souladu s tím, že v tomto případu není v oblasti splněna podmínka

>	Diff(P(x,y),y)=Diff(Q(x,y),x);

která je ekvivalentní s výrokem o nezávislosti křivkového integrálu na integrační cestě, viz.[1, V.7.6].

Pro kontrolu naznačené derivace spočteme

>	diff((x+y)^2,y)=diff(-(x-y)^2,x);

>

>