Příklad 1

Vypočtěte křivkový integrál druhého druhu [Maple OLE 2.0 Object]   podél křivky Gamma = AB .

>    restart:

Integrál spočteme třemi způsoby.

Zadáme úsečku

>    b:=[[2,3],[3,5]];

b := [[2, 3], [3, 5]]

Úsečku AB  můžeme parametrizovat například takto

>    _par:=x=2+t,y=3+2*t,t=0..1;
par:=2+t,3+2*t,t=0..1;

_par := x = 2+t, y = 3+2*t, t = 0 .. 1

par := 2+t, 3+2*t, t = 0 .. 1

# Druhý příkaz není zadán rovnicemi, protože  parametrizace v tomto tvaru je  lépe použitelná v následujících příkazech.

Dále určíme, zda je křivka Gamma  orientována souhlasně s parametrickým vyjádřením, tj. jde z bodu A  do bodu B . Dosadíme meze parametru t  do rovnic parametrizace.

>    subs(t=0,{_par[1],_par[2]});

{x = 2, y = 3}

# Jde o bod A. Použili jsme zadání parametrických rovnic s rovnicemi pro větší přehlednost

>    subs(t=1,{_par[1],_par[2]});

{x = 3, y = 5}

# Jde o bod B

Můžeme konstatovat, že křivka je orientována souhlasně s danou parametrizací. Ještě poznamenejme, že u všech dalších příkladů bude křivka souhlasně orientována s daným parametrickým vyjádřením. Pokud tomu bude jinak, bude na to upozorněno. V dalších příkladech už nebudeme orientaci ověřovat.

Nakreslíme nyní obrázek.
Nejprve pojmenujeme vektorové pole

>    vpole:=[x-y,x+y];

vpole := [x-y, x+y]

#   Integrand jako seznam

>    vplot := plots[fieldplot](vpole,x=-1..6,y=-1..6, grid=[10,10]):

#   Nakreslení vektorového pole pomocí funkce z rozšiřující knihovny plots .

>    par_p:=plot([par],-1..6,-1..6,thickness=5):

#   Vykreslení křivky. Užili jsme druhý zápis parametrických rovnic ve tvaru seznamu, protože přesně odpovídá požadavkům příkazu plot  na vykreslení křivky dané parametrickými rovnicemi.

>    p1:=plots[arrow]([2,3],[3,5],color=blue,difference=true):

#   Nakreslení orientace křivky

>    t1:=plots[textplot]([2,2.95,`A`],align=BELOW):

>    t2:=plots[textplot]([3,5.05,`B`],align=ABOVE):

#   Zápis textu do obrázku

>    plots[display]({vplot, par_p,t1,t2,p1});

[Maple Plot]

#  Vykreslení do jednoho obrázku

Dosadíme parametrické rovnice do integrandu

>    parpole:=[subs(_par[1],_par[2],vpole[1]),subs(_par[1],_par[2],vpole[2])];

parpole := [-1-t, 5+3*t]

#  Příkaz subs  provádí vícenásobnou substituci, substituční rovnice musí být zadány jako posloupnost, poslední parametr určuje místo použití.

Spočteme derivace

>    dpar:=diff([par[1],par[2]],t);

dpar := [1, 2]

Výpočet provedeme

>    Int(parpole[1]*dpar[1]+parpole[2]*dpar[2],t=0..1);

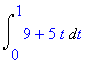
Int(9+5*t,t = 0 .. 1)

>    value(%);

23/2

Tento křivkový integrál II. druhu můžeme po dosazení parametrických rovnic zapsat pomocí skalárního součinu takto

>    Int((parpole.Diff([par[1],par[2]],t)), par[3]);

Int([-1-t, 5+3*t].Diff([2+t, 3+2*t],t),t = 0 .. 1)

Počítáme tedy integrál

>    Int(parpole.dpar, par[3]);

Int([-1-t, 5+3*t].[1, 2],t = 0 .. 1)

Jde o skalární součin dvou vektorů. Použijeme tedy příkaz dotprod  z rozšiřující knihovny linalg , který počítá skalární součin dvou vektorů.

>    arg:=linalg[dotprod](parpole,dpar);

arg := 9+5*t

# Argument integrálu

Počítáme integrál a výsledek je

>    Int(arg,par[3])=int(arg,par[3]);

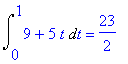
Int(9+5*t,t = 0 .. 1) = 23/2

Knihovna VectorCalculus  obsahuje pro výpočet skalárního součinu příkaz DotProduct , který však vyžaduje zadání vektorového pole, tj. pomocí <..>.

>    with(VectorCalculus): 

Warning, the assigned names <,> and <|> now have a global binding



Warning, these protected names have been redefined and unprotected: *, +, ., Vector, diff, int, limit, series

>    p_pole:=<parpole[1],parpole[2]>;

p_pole := Vector(%id = 14166864)

>    d_par:=<dpar[1],dpar[2]>;

d_par := Vector(%id = 14167064)

>    DotProduct(p_pole,d_par);

9+5*t

Tento způsob zápisu je nepříjemný, protože musí být nastavena správná soustava souřadnic. V našem případě kartézská, což zjistíme pomocí příkazu (více viz. příloha Knihovna VectorCalculus )

>    GetCoordinates();

cartesian

Nyní přejdeme k výpočtu pomocí příkazu LineInt . Nejprve musíme pracovat ve správné soustavě souřadnic, proto použijeme příkaz SetCoordinate , pomocí kterého danou soustavu nastavíme. V našem případě požaduje kartézskou soustavu proměnných x  a y ..

>    SetCoordinates(cartesian[x,y]);

cartesian[x,y]

# Připomeňme, že systém Maple má několik předdefinovaných soustav souřadnic. Více viz. příloha Knihovna VectorCalculus , popř. nápověda.

Vytvoříme vektorové pole, které získáme ze zadaného integrálu

>    vp:=VectorField(<x-y,x+y>);

vp := Vector(%id = 12588348)

Nyní užijeme příkaz LineInt  spolu s konstrukcí Line , která vytvoří úsečku pomocí dvou zadaných bodů.

>    LineInt(vp,Line(<2,3>,<3,5>));

23/2

V případě nesouhlasné orientace křivky s danou parametrizací dostáváme, v souladu s teorií, výsledek s opačným znaménkem.

>    LineInt(vp,Line(<3,5>,<2,3>));

-23/2

>   

>   

>   

>