Příklad 3

Spočtěte následující integrál podél prvního oblouku cykloidy

>	restart:with(plots):

Warning, the name changecoords has been redefined

>	Int([2*r-y,-(r-y)]*`.`,S=Gamma..``);

Parametrické rovnice prvního oblouku cykloidy jsou

>	_par:=x=r*(t-sin(t)),y=r*(1-cos(t)),t=0..2*Pi; par:=r*(t-sin(t)),r*(1-cos(t)),t=0..2*Pi;

Nakresleme obrázek

>	vpole:=[2*r-y,-r+y];

>	vplot := fieldplot(subs(r=1,vpole),x=-1..8,y=-1..3, grid=[10,10]):

#  Pro vykreslení obrázku je nutné pevně zvolené r , v našem případě jsme do obecného předpisu dosadili pomocí příkazu subs  jedničku.

>	p:=plot(subs(r=1,[par]),thickness=4):

# Graf prvního oblouku cykloidy

>	p1:=arrow([3,2],[3.2,2],difference=true,color=green,width=0.1,head_width=.3):

# Nakreslení orientace křivky

>	display({vplot,p,p1});

# Zobrazení do jednoho obrázku

• výpočet pomocí skalárního součinu

Dosazením parametrických rovnic do integrandů dostáváme

>	parpole:=[subs(_par[1],_par[2],vpole[1]),subs(_par[1],_par[2],vpole[2])];

#  Příkaz subs  provádí vícenásobnou substituci, tj. substituční rovnice musí být zadány jako posloupnost, poslední parametr určuje místo použití.

Přesný zápis integrálu se skalárním součinem tedy je

>	parpole:=simplify(parpole);

# Užili jsme funkci simplify  pro zjednodušení výrazů v identifikátoru parpole .

>	Int(simplify(parpole.Diff([par[1],par[2]],t)), par[3]);

Nyní provedeme naznačenou derivaci

>	dpar:=diff([par[1],par[2]],t);

# Provedli jsme derivaci prvních dvou prvků seznamu par

Počítáme tedy integrál

>	Int(parpole.dpar, par[3]);

Jde o skalární součin dvou vektorů. Použijeme příkaz dotprod   z rozšiřující knihovny linalg .

>	#assume(r>0); arg:=linalg[dotprod](parpole,dpar,'orthogonal');

# Argument integrálu

Počítáme tedy integrál a výsledkem je

>	Int(arg,par[3])=int(arg,par[3]);

• výpočet pomocí knihovny VectorCalculus

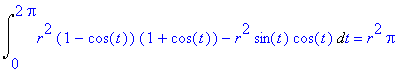
>	with(VectorCalculus):

Warning, the assigned names <,> and <|> now have a global binding

Warning, these protected names have been redefined and unprotected: *, +, ., Vector, diff, int, limit, series

>	vp:=VectorField(<vpole[1],vpole[2]>,cartesian[x,y]);

# Vytvoření vektorového pole

>	LineInt(vp,Path(<r*(t-sin(t)),r*(1-cos(t))>,t=0..2*Pi));

>

>

>