![x[T] := M[x](gamma)/s(gamma) = Int(y,s = gamma .. ``)/Int(1,s = gamma .. ``)](image/krint_1_pr101.gif)
Příklad 10
Vypočtěte těžiště části asteroidy v I. kvadrantu
| > | restart:with(student):with(plots):with(VectorCalculus): |
Warning, the name changecoords has been redefined
Warning, the assigned names <,> and <|> now have a global binding
Warning, these protected names have been redefined and unprotected: *, +, ., Vector, diff, int, limit, series
Souřadnice těžiště křivky jsou dány následujícími vztahy
| > | x[T]:=M[x](gamma)/s(gamma)= Int(y,s=gamma..``)/(Int(1,s=gamma..``)); y[T]:=M[y](gamma)/s(gamma)= Int(x,s=gamma..``)/(Int(1,s=gamma..``)); |
![y[T] := M[y](gamma)/s(gamma) = Int(x,s = gamma .. ``)/Int(1,s = gamma .. ``)](image/krint_1_pr102.gif)
Parametrické rovnice asteroidy v I. kvadrantu jsou
| > | par:=x=r*cos(t)^3,y=r*sin(t)^3,t=0..Pi/2; |
Nakresleme graf
| > | plot([cos(t)^3,sin(t)^3,t=0..2*Pi]): plot([cos(t)^3,sin(t)^3,t=0..Pi/2],color=blue, thickness=5): display({%,%%}); |
![[Maple Plot]](image/krint_1_pr104.gif)
Spočteme délku křivky
| > | s=Int(1,s=gamma..``); |
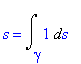
Dosazením parametrických rovnic do křivkového integrálu dostaneme
| > | s:=Lineint(1,par); |
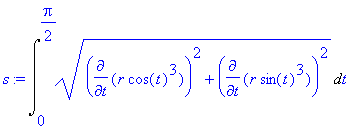
Přidáme ještě podmínku pro r a spočteme tento integrál
| > | assume(r>0); |
| > | sv:=simplify(value(%)); |
Dále spočtěme odpovídající momenty vzhledem k souřadným osám
| > | Mx:=Lineint(y,par): My:=Lineint(x,par): |
# Zadání integrálů
Určeme jejich hodnoty
| > | Mxv:=simplify(value(Mx)); Myv:=simplify(value(Mx)); |
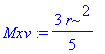
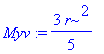
Nakonec dosadíme do vzorců pro výpočet souřadnic těžiště
| > | x[T]:=Mxv/sv; y[T]:=Myv/sv; |
![x[T] := 2/5*r](image/krint_1_pr1010.gif){kind=small}
![y[T] := 2/5*r](image/krint_1_pr1011.gif){kind=small}
Výpočet pomocí PathInt .
| > | _s:=simplify(PathInt(1,[x,y] = Path(<r*cos(t)^3,r*sin(t)^3>, t=0..Pi/2))); |
| > | _Mx:=simplify(PathInt(y,[x,y] = Path(<r*cos(t)^3,r*sin(t)^3>, t=0..Pi/2))); |
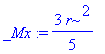
| > | _My:=simplify(PathInt(x,[x,y] = Path(<r*cos(t)^3,r*sin(t)^3>, t=0..Pi/2))); |
| > |
| > |
| > |
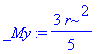