Příklad 2

Spočtěte křivkový integrál přes úsek paraboly y^2=2 x   vymezený průsečíky s parabolou x^2=2 y

>	restart:with(student):with(plots):with(VectorCalculus):

Warning, the name changecoords has been redefined

Warning, the assigned names <,> and <|> now have a global binding

Warning, these protected names have been redefined and unprotected: *, +, ., Vector, diff, int, limit, series

>	Int(y,s=gamma..``);

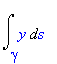
Nakreslení obrázku křivek - nutné zvolit pevné =1 .

>	p1:=implicitplot(y^2=2*1*x,x=-1..4,y=-1..4): p2:=implicitplot(x^2=2*1*y,x=-1..4,y=-1..4): p:=implicitplot(y^2=2*1*x,x=0..2,y=0..2,color=blue, thickness=6):

# Příkaz implicitplot  vykresluje křivky dané implicitně.

>	t1:=textplot([0.5,1.5,gamma]):

# Zapsání textu do obrázku

>	display({p1,p2,p,t1});

Zavedeme parametrizaci

>	par:=x=t^2/(2*rho),y=t,t=0..2*rho;

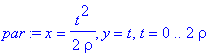
Počítáme tedy integrál

>	i:=Lineint(y,par);

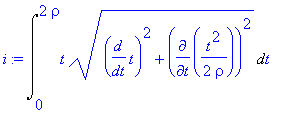
Výsledná hodnota je

>

value(i);

Výpočet pomocí  knihovny VectorCalculus

>	PathInt( y, [x,y] = Path(<t^2/(2*rho),t>,t=0..2*rho) );

# Využili jsme odvozené parametrizace a příkazu Path , která vytvoří požadovanou křivku. Tento příkaz vyžaduje nejméně dva parametry, prvním jsou parametrické rovnice křivky zadané jako vektor a druhým je rozsah daného parametru.

>

>

>

>

>