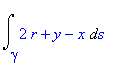
Příklad 3

Spočtěte křivkový integrál podél křivky x^2+y^2=r*y , jde o kružnici .

>	restart:with(student):with(plots):with(VectorCalculus):

Warning, the name changecoords has been redefined

Warning, the assigned names <,> and <|> now have a global binding

Warning, these protected names have been redefined and unprotected: *, +, ., Vector, diff, int, limit, series

>	Int(2*r+y-x,s=gamma..``);

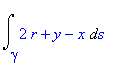
Nakreslení křivky - nutné zvolit pevné  r=1 .

>	implicitplot(x^2+y^2=1*y,x=-1..2*Pi,y=-1..2*Pi,numpoints=5000,          scaling=constrained);

# Parametr scaling  určuje měřítka na souřadnicových osách, CONSTRAINED (stejná), UNCONSTRAINED (různá). Parametr numpoints  zadán pro "hladké" vykreslení kružnice.

Křivku parametrizujeme známými rovnicemi

>	par:=x=r/2*cos(t),y=r/2+r/2*sin(t),t=0..2*Pi;

Počítáme tedy integrál

>	Lineint(2*r+y-x,par);

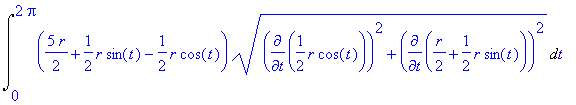
Výsledkem je

>	v:=value(%);

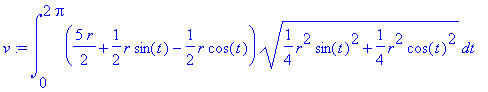
Systém Maple neumí tento integrál spočítat přímo, ale po zavedení známé rovnice a požadavku na  r>0   vše dopočítá

>	assume(r>0);

# Přidá podmínku pro hodnoty r .

>	simplify(v,{sin(t)^2+cos(t)^2=1});

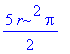
# Pomocí druhého parametru je možné zadat rovnice, kterými Maple zjednoduší výraz zadaný prvním parametrem.

Připomeňme ještě možnost odstranění podmínky na r .

>

r:='r';

# Následující příkaz ukazuje, že podmínka na r  byla odstraněna.

>	simplify(v,{sin(t)^2+cos(t)^2=1});

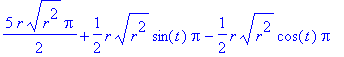
Výpočet pomocí  knihovny VectorCalculus

>	PathInt( 2*r+y-x, [x,y] = Path(<r/2*cos(t),r/2+r/2*sin(t)>, t=0..2*Pi) );

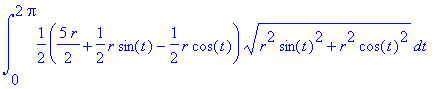
# Využili jsme odvozené parametrizace a příkazu Path , která vytvoří požadovanou křivku

>	PathInt( 2*r+y-x, [x,y] = Circle(<0,r/2>,r/2) );

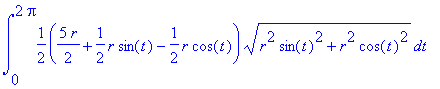
# Jiné určení křivky a to pomocí konstrukce Circle(střed, poloměr)

>

>

>