Příklad 9

Spočtěte hmotnost části elipsy v I. kvadrantu, je-li délková hustota  v každém bodě elipsy rovna y -ové souřadnici daného bodu.

>	restart:with(student):with(plots):with(VectorCalculus):

Warning, the name changecoords has been redefined

Warning, the assigned names <,> and <|> now have a global binding

Warning, these protected names have been redefined and unprotected: *, +, ., Vector, diff, int, limit, series

Hmotnost křivky     je dána integrálem

>	m(Gamma)=Int(mu(x,y),s=Gamma..``);

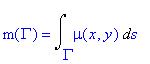
Parametrické rovnice části elipsy v I. kvadrantu jsou

>	par:=x=a*cos(t),y=b*sin(t),t=0..Pi/2;

Nakresleme obrázek, zvolme a=2 , b=1

>	p:=plot([2*cos(t),1*sin(t),t=0..2*Pi]): p1:=plot([2*cos(t),1*sin(t),t=0..Pi/2],thickness=5, color=blue):

# Parametr thickness  určuje šířku pera pro vykreslení křivky.

>	display({p,p1}, scaling=constrained);

Zapišme křivkový integrál

>	i:=Lineint(y,par);

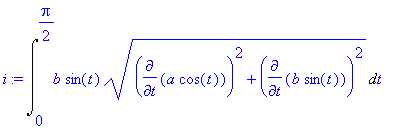
# První parametr příkazu zastupuje integrand, kterým v tomto případě je délková hustota, dle zadání y .

Pro upravení integrálu je třeba zadat podmínky pro parametry a , b

>	assume(a>0);assume(b>0);

Výsledná hmotnost je

>

value(i);

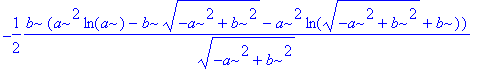
Ukažme, jak bychom sami postupovali při výpočtu integrálu i

>	i1:=simplify(i);

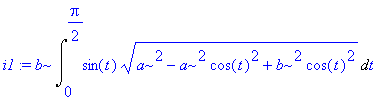
Zavedeme substituci

>	changevar(u=cos(t),i1,u);

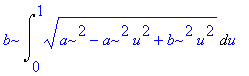
# Příkaz je obsažen ve student  package. Prvním parametrem je rovnice pro substituci, druhým integrál nebo sumace, do které substituci chceme dosadit, třetím parametrem je nová proměnná.

Tento integrál je tabulkovým integrálem. Spočteme ho pomocí systému Maple

>

value(%);

Výpočet pomocí PathInt .

>	PathInt(y,[x,y] = Path(<a*cos(t),b*sin(t)>,t=0..Pi/2));

>
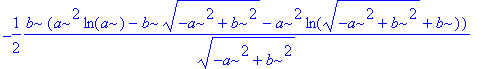