Příklad 8

Spočtěte délku kardioidy

>    restart:with(student):with(plots):with(VectorCalculus): 

Warning, the name changecoords has been redefined



Warning, the assigned names <,> and <|> now have a global binding



Warning, these protected names have been redefined and unprotected: *, +, ., Vector, diff, int, limit, series

Parametrické rovnice jsou

>    par:=x=r*(1+cos(t))*cos(t),y=r*(1+cos(t))*sin(t),
t=0..2*Pi;

par := x = r*(cos(t)+1)*cos(t), y = r*(cos(t)+1)*sin(t), t = 0 .. 2*Pi

Nakreslíme graf křivky pro r=1

>    plot([1*(1+cos(t))*cos(t),1*(1+cos(t))*sin(t),par[3]]);

[Maple Plot]

# Křivka zadaná parametricky, proto je nutné užít [...].

Definice křivkového integrálu předpokládá křivku hladkou, popř. po částech hladkou. Je tedy nutné rozdělit kardioidu na dvě hladké křivky. Proto budeme počítat integrál např. jen v horní polorovině. Počítáme tedy křivkový integrál

>    i:=Lineint(1,par[1],par[2],t=0..Pi);

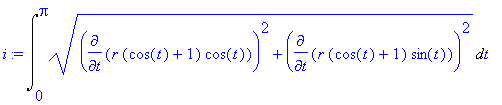
i := Int((diff(r*(cos(t)+1)*cos(t),t)^2+diff(r*(cos(t)+1)*sin(t),t)^2)^(1/2),t = 0 .. Pi)

# Zde jsme museli užít volání jednotlivých členů posloupnosti, protože byl zvolen jiný rozsah parametru t .

Podmínka na r

>    assume(r>0);

Délka křivky v horní polorovině je

>    value(i);

4*r

Protože jsme uvažovali pouze horní polorovinu, výsledná délka křivky je

>    vysledek:=2*value(i);

vysledek := 8*r

Výpočet pomocí PathInt .

>    PathInt(1,[x,y] = Path(<r*(1+cos(t))*cos(t),r*(1+cos(t))*sin(t)>,
t=0..2*Pi));

8*r

# Tento příkaz provede výpočet i při zadání po částech hladké  křivky

>   

>