Příklad 11

Určete statický moment 1. závitu kuželové šroubovice vzhledem k souřadnicové rovině xy , je-li délková hustota v každém bodě křivky rovna kvadrátu vzdálenosti od roviny xy .

>	restart:with(student):with(plots):with(VectorCalculus):

Warning, the name changecoords has been redefined

Warning, the assigned names <,> and <|> now have a global binding

Warning, these protected names have been redefined and unprotected: *, +, ., Vector, diff, int, limit, series

První statický moment vzhledem k souřadnicové rovině xy  je definován jako

>	M[xy]=Int(z*mu(x,y,z),s=gamma..``);

kde  je délková hustota. Analogicky definujeme zbylé dva momenty.

Parametrické rovnice kuželové šroubovice

>	x=t*cos(t);y=t*sin(t);z=v*t;t=0..2*Pi;

Pro jednoduchost položme v=1

>	par:=x=t*cos(t),y=t*sin(t),z=t,t=0..2*Pi;

Nakresleme obrázek

>	p:=spacecurve([t*cos(t),t*sin(t),t],t=0..6*Pi, axes=normal):

# Kuželová šroubovice je křivka v prostoru, proto byl použit tento příkaz. Parametr axes  určuje zobrazení souřadnicového systému.

>	p1:=spacecurve([t*cos(t),t*sin(t),t],t=0..2*Pi, numpoints=10000,axes=normal,color=blue,thickness=5):

# Zvýraznění prvního závitu šroubovice, parametr numpoints  uveden z důvodu "hladšího" zobrazení křivky.

>	display({p,p1});

Zapišme křivkový integrál s přihlédnutím na zadanou délkovou hustotu, která je dána kvadrátem vzdálenosti bodu od roviny xy .

>	i:=Lineint(z*z^2,par);

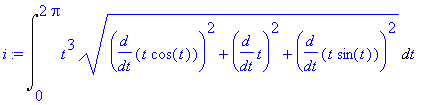
Výsledný moment vzhledem k souřadnicové rovině xy  je roven

>

value(i);

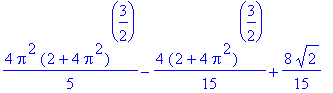
Numericky spočteme integrál pomocí

>

evalf(i);

Výpočet pomocí PathInt .

>	PathInt(z^3,[x,y,z] = Path(<t*cos(t),t*sin(t),t>,t=0..2*Pi));

>
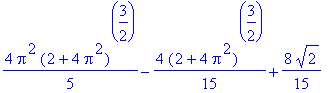