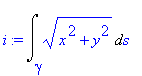
Příklad 4

Spočtěte křivkový integrál po oblouku evolventy kružnice

>    restart:with(student):with(plots):with(VectorCalculus): 

Warning, the name changecoords has been redefined



Warning, the assigned names <,> and <|> now have a global binding



Warning, these protected names have been redefined and unprotected: *, +, ., Vector, diff, int, limit, series

>    i:=Int(sqrt(x^2+y^2),s=gamma..``);

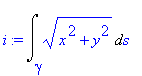
i := Int((x^2+y^2)^(1/2),s = gamma .. ``)

Rovnice evolventy kružnice

>    par:=x=r*(cos(t)+t*sin(t)),y=r*(sin(t)-t*cos(t)),
t=0..2*Pi;

par := x = r*(cos(t)+t*sin(t)), y = r*(sin(t)-t*cos(t)), t = 0 .. 2*Pi

Vykresleme graf pro pevně zvolené  r=2 .

>    plot([2*(cos(t)+t*sin(t)),2*(sin(t)-t*cos(t)),
t=0..2*Pi]);

[Maple Plot]

# Pro vykreslení křivky dané parametricky je nutné parametrické rovnice zapsat jako seznam, tj. do [...].

Dosaďme do křivkového integrálu

>    Lineint(sqrt(x^2+y^2),par);

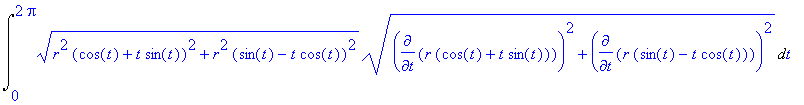
Int((r^2*(cos(t)+t*sin(t))^2+r^2*(sin(t)-t*cos(t))^2)^(1/2)*(diff(r*(cos(t)+t*sin(t)),t)^2+diff(r*(sin(t)-t*cos(t)),t)^2)^(1/2),t = 0 .. 2*Pi)

Zjednodušíme

>    simplify(%);

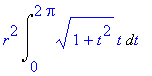
r^2*Int((1+t^2)^(1/2)*t,t = 0 .. 2*Pi)

Výslednou hodnotu dostaneme výpočtem předchozího integrálu

>    v:=value(%);

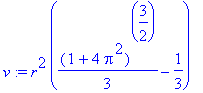
v := r^2*(1/3*(1+4*Pi^2)^(3/2)-1/3)

Výpočet pomocí PathInt .

>    v1:=PathInt(sqrt(x^2+y^2),[x,y] = Path(<r*(cos(t)+t*sin(t)),
r*(sin(t)-t*cos(t))>,t=0..2*Pi));

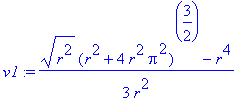
v1 := 1/3*((r^2)^(1/2)*(r^2+4*r^2*Pi^2)^(3/2)-r^4)/r^2

>    is(simplify(v1)=simplify(v));

true

# Kontrola, že jde o stejný výraz

>   

>   

>