Příklad 12

Vypočtěte plošný obsah části válcové plochy x^2+y^2=r^2  omezené rovinnou z=0 , a plochou z=r-x^2/r .

>    restart:with(student):with(plots):with(VectorCalculus): 

Warning, the name changecoords has been redefined



Warning, the assigned names <,> and <|> now have a global binding



Warning, these protected names have been redefined and unprotected: *, +, ., Vector, diff, int, limit, series

Nakresleme obrázek

>    p:=implicitplot3d(x^2+y^2=1,x=-1..2,y=-1..2,
z=-1..2,color=red,style=hidden):

# Parametr style  určuje grafické zobrazení plochy, hodnota hidden  skryje mřížku.  

>    p1:=plot3d(0,x=-1..2,y=-1..2,color=green):

>    p2:=plot3d(1-x^2,x=-1..2,y=-1..2,color=yellow):

>    display({p,p1,p2},axes=normal);

[Maple Plot]

# Parametr axes  určuje zobrazení souřadnicového systému.

V tomto případě je řídící křivkou kružnice s parametrickým vyjádřením

>    par:=x=r*cos(t),y=r*sin(t),t=0..2*Pi;

par := x = r*cos(t), y = r*sin(t), t = 0 .. 2*Pi

Počítáme plošný obsah válcové plochy , tedy integrál

>    S:=Int(h(x,y)-g(x,y),s=gamma..``);

S := Int(h(x,y)-g(x,y),s = gamma .. ``)

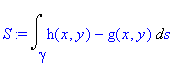
kde h(x,y)  je "horní" a g(x,y)  "dolní" plocha. V našem případě je g(x,y)=0 , h(x,y)=r-x^2/r . Horní plochu musíme převést pomocí zvolené parametrizace. Výsledkem je

>    z:=r-r^2*cos(t)^2/r=r*sin(t)^2;
z:=r*sin(t)^2;

z := r-r*cos(t)^2 = r*sin(t)^2

z := r*sin(t)^2

Dosaďme nyní do integrálu

>    i:=Lineint(z,par);

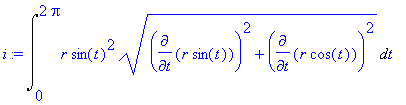
i := Int(r*sin(t)^2*(diff(r*sin(t),t)^2+diff(r*cos(t),t)^2)^(1/2),t = 0 .. 2*Pi)

Výsledkem je

>    i1:=value(i);

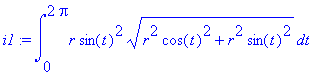
i1 := int(r*sin(t)^2*(r^2*cos(t)^2+r^2*sin(t)^2)^(1/2),t = 0 .. 2*Pi)

Musíme upravit výraz pod odmocninou a výsledkem je

>    assume(r>0);

>    simplify(i1,{sin(t)^2+cos(t)^2=1});

Pi*r^2

# Vymezení konstanty a zjednodušení pomocí vlastního vzorce.

Výpočet pomocí PathInt .

>    PathInt(z,[x,y] = Path(<r*cos(t),r*sin(t)>,t=0..2*Pi));

Pi*r^2

>   

>   

>