Příklad 13

Nalezněte těžiště 1. závitu šroubovice

>	restart:with(student):with(plots):with(VectorCalculus):

Warning, the name changecoords has been redefined

Warning, the assigned names <,> and <|> now have a global binding

Warning, these protected names have been redefined and unprotected: *, +, ., Vector, diff, int, limit, series

Parametrické rovnice jsou

>	par:=x=r*cos(t),y=r*sin(t),z=v*t,t=0..2*Pi;

Vykreslíme tuto křivku, položme v=3, r=2 .

>	spacecurve([2*cos(t),2*sin(t),3*t],t=0..2*Pi, axes=normal,thickness=5);

Potřebné integrály jsou:

- délka křivky

>	s[gamma]:=Lineint(1,par);

# Pomocí [...] je zapsán pouze index.

>	value(s[gamma]);

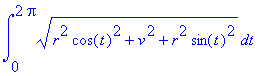
Potřebujeme upravit výraz pod odmocninou

>	sg:=simplify(%,{cos(t)^2+sin(t)^2=1});

# Druhý parametr určuje rovnice, pomocí kterých se výraz zjednoduší.

Výpočet pomocí PathInt .

>	_s:=PathInt(1,[x,y,z] = Path(<r*cos(t),r*sin(t),v*t>, t=0..2*Pi));

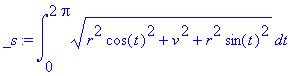
# Dále lze stejně upravit jako při výpočtu pomocí Lineint

- první statické momenty

>	M[x,y]:=Lineint(z,par);

>	M[y,z]:=Lineint(x,par);

>	M[x,z]:=PathInt(y,[x,y,z] = Path(<r*cos(t),r*sin(t),v*t>, t=0..2*Pi));

# Pomocí příkazu PathInt  dostáváme hned výsledek.

>

Vypočítejme hodnoty uvedených integrálů

>	Mxy:=value(M[x,y]); Myz:=value(M[y,z]); Mxz:=value(M[x,z]);

Z výsledků je patrné, že těžiště leží na souřadnicové ose z , což je očekávaný výsledek. Zbývá určit jeho z -tovou souřadnici.

>	z[T]:=Mxy/sg;

>

>