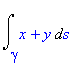
Příklad 1

Spočtěte následující křivkový integrál po po částech hladké křivce, která je zadána třemi vrcholy trojúhelníka.

>    Int(x+y,s=gamma..``);

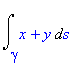
Int(x+y,s = gamma .. ``)

>    body:=[[1,-1],[2,-1],[1,0]];

body := [[1, -1], [2, -1], [1, 0]]

>    with(plots):

# Pro vykreslení křivky a její popis je nutné nahrát tuto knihovnu do paměti

>    tr:=polygonplot(body):

# Příkaz pro vykreslení oblasti zadané  bodově

>    t1:=textplot([1.3,-1.05,gamma_1],align={ABOVE,RIGHT}):
t2:=textplot([1.5,-0.5,gamma_2],align={ABOVE,RIGHT}):
t3:=textplot([0.8,-0.5,gamma_3],align={ABOVE,RIGHT}):
_t1:=textplot([0.95,-1.01,A],align={ABOVE,RIGHT}):
_t2:=textplot([2.05,-1,B],align={ABOVE,RIGHT}):
_t3:=textplot([0.95,-0.05,C],align={ABOVE,RIGHT}):

# Příkaz textplot  se užívá k zápisu textu do obrázku

>    display({tr,t1,t2,t3,_t1,_t2,_t3});

[Maple Plot]

# Zobrazení grafu a textu do jednoho obrázku

>   

Z obrázku je vidět, že jde opravdu o křivku po částech hladkou, proto integrál rozdělíme na tři dílčí integrály po jednotlivých hladkých křivkách. Na výpočtu integrálu přes křivky gamma_1, tj. úsečka AB, si ukážeme jednotlivé kroky, které pak budeme považovat za jasné.

Nejprve je třeba určit parametrizaci křivky gamma_1. Jde o úsečku AB a jednou z možných parametrizací je

>    par1:=x=1+t,y=-1,t=0..1;

par1 := x = 1+t, y = -1, t = 0 .. 1

# Identifikátoru par1  jsem přiřadili  posloupnost parametrických rovnic, tzn. při každém dalším použití par1  bude na jeho místo vložena tato posloupnost.

Dosadíme do křivkového integrálu, tj. počítáme

>    i1:=Lineint(x+y,par1);

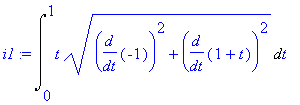
i1 := Int(t*(diff(-1,t)^2+diff(1+t,t)^2)^(1/2),t = 0 .. 1)

Určíme hodnotu tohoto integrálu pomocí příkazu

>    value(i1);

1/2

Určeme nyní parametrizace zbylých dvou křivek

>    par2:=x=2-t,y=-1+t,t=0..1;

par2 := x = 2-t, y = -1+t, t = 0 .. 1

>    par3:=x=1,y=-1+t,t=0..1;

par3 := x = 1, y = -1+t, t = 0 .. 1

Dosadíme do integrálu

>    i2:=Lineint(x+y,par2[1],par2[2],par2[3]):

>    i3:=Lineint(x+y,par3[1],par3[2],par3[3]):

Určíme hodnoty a sečteme jednotlivé integrály

>    value(i1+i2+i3);

1+2^(1/2)

Nyní se podívejme na výpočet s využitím funkcí z rozšiřující knihovny VectorCalculus . Vysvětlíme pouze základní pojmy a postupy, více naleznete v příloze Knihovna VectorCalculus .

Nejprve určíme křivku. Máme zadán trojúhelník pomocí tří bodů. Užijeme konstrukce LineSegments , která ze zadaných bodů vytvoří  po částech lineární křivku.

>    with(VectorCalculus): 

Warning, the assigned names <,> and <|> now have a global binding



Warning, these protected names have been redefined and unprotected: *, +, ., Vector, diff, int, limit, series

>    l:=LineSegments( <1,-1>, <2,-1>,<1,0> ,<1,-1>);

l := LineSegments(Vector(%id = 2869412),Vector(%id = 12468860),Vector(%id = 2697136),Vector(%id = 12468900))

# Je potřeba zadat čtyři body, protože každá úsečka je dána dvěma body a my potřebujeme získat trojúhelník.

Dále pro výpočet užijeme příkaz PathInt , která počítá integrál I. druhu.

>    PathInt( x+y, [x,y] = l );

1+2^(1/2)

Jak je vidět, tento postup je velmi efektivní, ale je potřeba dávat pozor na zadání křivky.

>   

>   

>