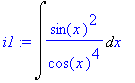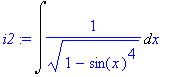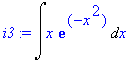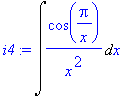Primitivní funkce pomocí knihovny student v systému Maple - Matematické výpočty v systému Maple

Primitivní funkce pomocí knihovny student

Postup při výpočtu primitivní funkce lze také vysvětlit při použití rozšiřující knihovny student . Jsou v ní uvedeny příkazy intparts , changevar , pro dva základní postupy, metodu per partes a metodu substituční.

Metoda per partes

Metoda vychází z matematických vzorců

(1)

nebo

(2)

kde F , G jsou primitivní funkce k funkcím f , g . V obou případech se počítá integrál na levé straně a volí se ten ze vzorců, ve kterém výpočet integrálu na pravé straně a primitivní funkce G(x) , popř. F(x) není náročný, anebo je méně náročný.

Příkaz určený pro výpočet metodou per partes má tvar

intparts( Int(h(x),x) , k(x) ) , kde (viz. levé strany vztahů (1), (2) ) a při užití vztahu (1), popř. při užití druhého vztahu. k(x) je tedy vždy ta funkce, kterou chceme derivovat.

Příkaz pro výpočet metodou per partes může mít i obecnější tvar

intparts(Z(x,y),k(x)) , kde Z(x,y) je výraz pro výpočet hodnoty funkce Z dvou proměnných a .

Ještě připomeňme, že tento příkaz je součástí rozšiřující knihovny student. Proto je nutné knihovnu nahrát do paměti.

> restart:with(student):
# nahrání rozšiřující knihovny

Řešené příklady

Příklad 1

Příklad 2

Příklad 3

Příklad 4

Příklad 5

Příklad 6

Metoda substituční

Metoda vychází z matematických vzorců

(3)

nebo

(4)

Příkaz pro výpočet substituční metodou má tvar

changevar(relace, Int(g(x),x), nová proměnná) , kde relace je vztah tvaru

mezi starou proměnnou x a novou proměnnou t . V případě relace, v níž je nová proměnná uvedena v relaci pouze na pravé straně, nemusí být třetí parametr uveden.

Ještě připomeňme, že tento příkaz je součástí rozšiřující knihovny student. Proto je nutné knihovnu nahrát do paměti.

> restart:with(student):
# nahrání rozšiřující knihovny