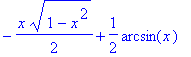Příklad 7

>	restart:with(student):

>	i7:=Int(x^2/sqrt(1-x^2),x);

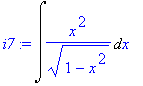
Integrand upravíme tak, že přičteme a odečteme v čitateli 1 a zlomek rozdělíme na dva

>	p:=(x^2-1)/sqrt(1-x^2)+1/sqrt(1-x^2);

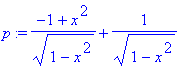
Jednotlivé zlomky označíme

>	p1:=(-1+x^2)/(1-x^2)^(1/2)=-sqrt(1-x^2); p2:=1/((1-x^2)^(1/2)):

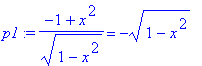
Počítáme tedy integrál

>	i7u:=Int(rhs(p1),x)+Int(p2,x);

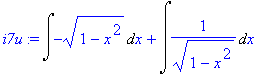
Provedeme kontrolní výpočet, zda jde o stejné integrály

>	is(value(i7)=value(i7u));

Druhý integrál z i7u  nalezneme přímo v tabulkách základních integrálů a označíme jej

>	i7u2:=arcsin(x):

Při výpočtu prvního integrálu, označíme ho i7u1 , zavedeme substituci  pro .

>	i7u1:=Int(-sqrt(1-x^2),x);

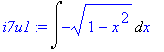
>	i7u1_:=changevar(sin(t)=x,i7u1,t);

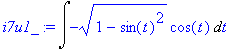
Zjednodušíme pomocí známého vzorce pro součet druhé mocniny sin  a cos . Dostaneme

>	assume(-Pi/2<t,t<Pi/2);        # upraven obor proměnné t, dle výše uvedené substituce

>	i7u1_:=simplify(i7u1_);

Dále užijeme vzorce pro výpočet polovičního úhlu

>	i7u1_:=subs(cos(t)^2=1/2*(1+cos(2*t)),i7u1_);

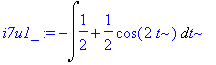
Tento integrál už lze snadno spočítat

>	v:=value(i7u1_);

Předchozí výsledek zjednodušíme

>	simplify(v,{sin(2*t)=2*cos(t)*sin(t)});

Vrátíme se k původní proměnné x  substitucí  

>	i7u1:=simplify(subs(t=arcsin(x),%));

A tedy výsledný integrál je roven

>	i7=simplify(i7u1+i7u2);

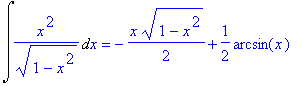
Provedeme kontrolu výpočtu

>	value(i7);