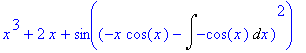Příklad 1

Vypočtěte následující integrál metodou per partes

>	i0:=Int(x*sin(x),x);

>	i0=intparts(i0,x);                 # výpočet - za nederivovanou složku volíme x

Použili jsme vzorec (1) pro  f(x)=x , g(x)=sin(x) . Vidíme, že výpočet integrálu na pravé straně je již snadný. Stejně tak výpočet primitivní funkce G(x) byl snadný.

>	i0=intparts(i0,sin(x));

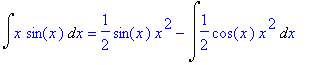
Použili jsme zde vzorec (2) pro f(x)=x  a g(x)=sin(x) . Vidíme, že výpočet integrálu na pravé straně je náročnější než výpočet původního integrálu.

>	i0=intparts(i0,1);

Opět jsme použili vzorec (2) pro f(x)=x sin(x)  a g(x)=1 . Výpočet primitivní funkce F(x)  je náročný, ve skutečnosti se jedná o výpočet původního integrálu. Porovnejme poslední variantu s výsledkem příkazu pro výpočet primitivní funkce bez použití příkazu intparts :

>	i0=int(integrand(i0),x);

Pomocí příkazu integrand  z rozšiřující knihovny student  získáme integrand z daného integrálu.

Dále ukážeme použití příkazu intparts  v obecnějším tvaru

>	intparts(x^3+2*x+sin(i0^2),x);