Příklad 4
| > | i3:=Int(x^3*cos(x^2),x); |
![]()
Za funkci k(x) volíme x^2 . Jiné volby by nevedly k cíli.
| > | intparts(i3,x); # tato volba nevede k cíli |
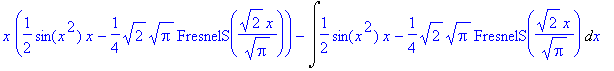
| > | i3=intparts(i3,x^2); # jediná volba, která vede k cíli |
![]()
Výpočet integrálu na pravé straně lze již snadno provést substituční metodou ( viz. následující odstavec).
| > | intparts(i3,x^3); # opět nevede k cíli |
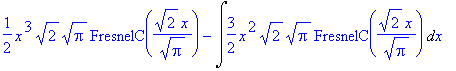
| > |