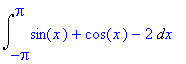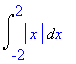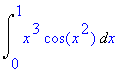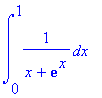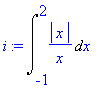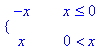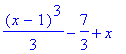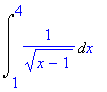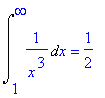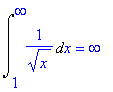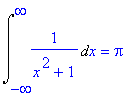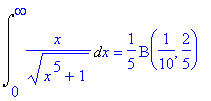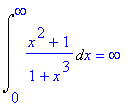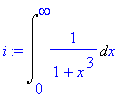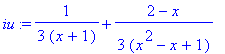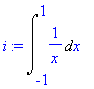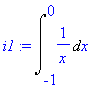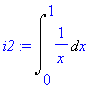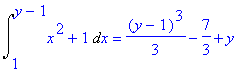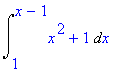Riemannův integrál v systému Maple

V této kapitole probereme Riemannovy integrály:

V předchozích dvou kapitolách byly popsány příkazy int(f(x),x) a Int(f(x),x) pro primitivní funkce a příkazy
intparts(Int(h(x),x),k(x))
a
changevar(relace,Int(g(x),x), nová_proměnná)
z knihovny student pro výpočet primitivní funkce metodou per partes a metodou substituční. Všechno, co bylo uvedeno o těchto příkazech, včetně použití příkazu value, se přenáší i na příkazy int, Int, intparts a changevar pro výpočet a zápis Riemannova integrálu a nevlastního integrálu. Rozdíl je pouze v tom, že se v příkazech dodá informace o mezích.

Příkazy pak mají tvar

int( f(x), x=dolní mez .. horní mez )
Int( f(x), x=dolní mez .. horní mez )
intparts( Int(h(x),x= dolní mez .. horní mez), k(x) )
changevar( relace, Int( g(x),x= dolní mez .. horní mez), nová proměnná )

Jako meze mohou být uvedeny libovolné výrazy. Mohou být i nevlastní (-infinity, infinity) a integrand může mít singularity

Vlastní Riemannův integrál

> restart:with(student):

Příklad 1

> f:=x->sin(x)+cos(x)-2;

> Int(f(x),x=-Pi..Pi);
# matematický zápis

> value(%);
# vypočtená hodnota

Příklad 2

> Int(abs(x),x=-2..2);

> value(%);

Příklad 3

> Int(x^3*cos(x^2),x=0..1);

> value(%);

Příklad 4

> int(1/(x+exp(x)),x=0..1);

Maple tento integrál neumí spočítat analyticky. My to také neumíme. Proto místo výsledku výpočtu vypíše pouze matematický zápis tohoto integrálu.

Příklad 5

> restart:with(student):

> i:=Int(abs(x)/x,x=-1..2);

> int(integrand(i),x);
# výpočet primitivní funkce pomocí funkce integrand z knihovny student

> value(i);

Více naleznete v kompletním exportu souboru *.mws na této stránce.

Nevlastní Riemannův integrál

Příklad 12

> Int(1/sqrt(x-1),x=1..4);

> value(%);

Jedná se o nevlastní integrál. Integrand má singularitu v bodě 1.

Příklad 13

Určíme, zda dané integrály konvergují či divergují

> Int(1/x^3,x=1..infinity)=
int(1/x^3,x=1..infinity);

> Int(1/sqrt(x),x=1..infinity)=
int(1/sqrt(x),x=1..infinity);

> Int(1/(x^2+1),x=-infinity..infinity)=
int(1/(x^2+1),x=-infinity..infinity);

> Int(x/sqrt(x^5+1),x=0..infinity)=
int(x/sqrt(x^5+1),x=0..infinity);

> Int((x^2+1)/(x^3+1),x=0..infinity)=
int((x^2+1)/(x^3+1),x=0..infinity);

Příklad 14

> restart:with(student):

> i:=Int(1/(1+x^3),x=0..infinity);

Rozložíme integrand na parciální zlomky. Pomocí příkazu integrand získáme integrand předchozího integrálu.

> iu:=convert(integrand(i),parfrac,x);

Spočteme primitivní funkci

> iu1:=int(iu,x);

Dle Leibnitz-Newtonovy věty dosadíme meze. Pro infinity musíme počítat limitu.

> limit(iu1,x=infinity)-simplify(subs(x=0,%));

Kontrola výpočtu

> value(i);

Příklad 15

> i:=Int(1/x,x=-1..1);

Problémem při integraci je neodstranitelná singularita v bodě 0. Proto rozdělíme integrál na dva a pokud oba konvergují, pak jejich součet je právě hledaným integrálem.

> i1:=Int(1/x,x=-1..0);

> i2:=Int(1/x,x=0..1);

Spočítáme limitu pro x jdoucí k 0 z leva pro první z dílčích integrálů.

> limit(value(i1),x=0,left);

Limita je nevlastní, a proto i původní integrál diverguje.

> value(i);

Riemannův integrál s proměnnými mezemi

Integrály s proměnnými mezemi využijeme později při výpočtu vícenásobných integrálů

> Int(x^2+1,x=1..y-1)=int(x^2+1,x=1..y-1);

Následující příklad ukáže, že systém Maple se správně vyrovná i s kolizí označení, kdy proměnnou v horní mezi označíme stejným písmenkem x jako integrační proměnnou.

> Int(x^2+1,x=1..x-1);

> value(%);

Ing. Vladimír Žák

MAPLE

Matematika

Knihovny

Informace

Vlastní Riemannův integrál

Více naleznete v kompletním exportu souboru *.mws na této stránce.

Nevlastní Riemannův integrál

Riemannův integrál s proměnnými mezemi