Příklad 1
| > | f:=x->sin(x)+cos(x)-2; |
![]()
| > | Int(f(x),x=-Pi..Pi); # matematický zápis |
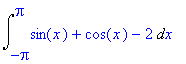
| > | value(%); # vypočtená hodnota |
![]()
Matematické výpočty v programu Maple
Ing. Vladimír Žák
email : zakyn@centrum.cz
web: http://www.vladimirzak.com
Soubor vznikl s podporou grantového projektu FRVŠ 3323/2006
Riemannův a nevlastní Riemannův integrál
V předchozích dvou kapitolách byly popsány příkazy int(f(x),x) a Int(f(x),x) pro primitivní funkce a příkazy intparts(Int(h(x),x),k(x)) a changevar(relace,Int(g(x),x),nová proměnná) z knihovny student pro výpočet primitivní funkce metodou per partes a metodou substituční. Všechno, co bylo uvedeno o těchto příkazech, včetně použití příkazu value , se přenáší i na příkazy int , Int , intparts a changevar pro výpočet a zápis Riemannova integrálu a nevlastního integrálu. Rozdíl je pouze v tom, že se v příkazech dodá informace o mezích.
Příkazy pak mají tvar
int( f(x), x=dolní mez .. horní mez )
Int( f(x), x=dolní mez .. horní mez )
intparts( Int(h(x),x= dolní mez .. horní mez), k(x) )
changevar( relace, Int( g(x),x= dolní mez .. horní mez), nová proměnná )
Jako meze mohou být uvedeny libovolné výrazy. Mohou být i nevlastní (- infinity , infinity ) a integrand může mít singularity.
| > | restart:with(student): |
Příklad 1
| > | f:=x->sin(x)+cos(x)-2; |
![]()
| > | Int(f(x),x=-Pi..Pi); # matematický zápis |
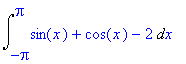
| > | value(%); # vypočtená hodnota |
![]()
| > |
Příklad 2
| > | Int(abs(x),x=-2..2); |
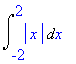
| > | value(%); |
![]()
| > |
Příklad 3
| > | Int(x^3*cos(x^2),x=0..1); |
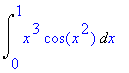
| > | value(%); |
![]()
| > |
Příklad 4
| > | int(1/(x+exp(x)),x=0..1); |
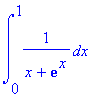
Maple tento integrál neumí spočítat analyticky. My to také neumíme. Proto místo výsledku výpočtu vypíše pouze matematický zápis tohoto integrálu.
| > |
Příklad 5
| > | restart:with(student): |
| > | i:=Int(abs(x)/x,x=-1..2); |
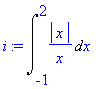
| > | int(integrand(i),x); # výpočet primitivní funkce |
![PIECEWISE([-x, x <= 0],[x, 0 < x])](image/riemann_komplet10.gif)
| > | value(i); |
![]()
| > |
Metoda per partes
Při výpočtu použijeme příkaz intparts
Příklad 6
Metoda per partes
| > | with(student): |
| > | Int(x*cos(x),x=0..Pi/2); |
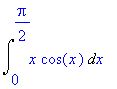
Integrál vypočteme metodou per partes
| > | intparts(%,x); # za nederivovanou složku vezmeme x |
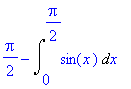
Tento integrál již snadno spočítáme
| > | value(%); |
![]()
| > |
Příklad 7
| > | i:=Int(exp(x)*cos(x),x=0..Pi); |
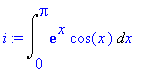
Použijeme metodu per partes
| > | intparts(i,cos(x)); |
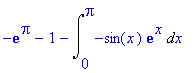
Ještě jednou
| > | intparts(%,sin(x)); |
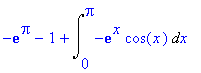
Zjednodušíme a položíme do rovnice.
| > | i=simplify(%); |
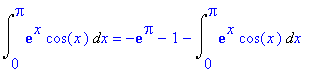
Integrál z rovnice vyjádříme
| > | isolate(%,i); |
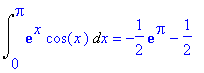
| > | value(i); # přímý výpočet |
![]()
| > |
| > |
Substituční metoda
Při výpočtu použijeme příkaz changevar
Příklad 8
| > | restart:with(student): |
| > | i1:=Int(x^2*sqrt(1-x^2),x=0..1); |
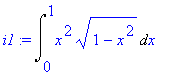
Použijeme substituci x = sin(t) . Jak je vidět z následujícího výsledku operace, systém Maple přepočítá i integrační meze.
| > | i1s:=changevar(x=sin(t),i1,t); |
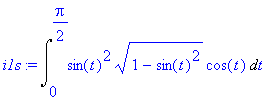
Počítáme tedy integrál
| > | i1u:=Int(sin(t)^2*cos(t)^2,t = 0 .. 1/2*Pi); |
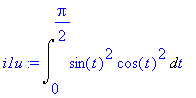
Použijeme známé vzorce pro sin a cos
| > | simplify(i1u,{sin(t)^2=1/2*(1- cos(2*t)),cos(t)^2=1/2*(1+cos(2*t))}); |
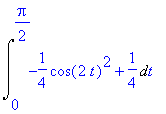
Výše uvedený integrál snadno spočítáme pomocí vzorce pro dvojnásobný argument funkce cos . Užili jsme ho už v předchozím kroku
| > | value(%); |
![]()
| > |
| > |
Příklad 9
| > | restart:with(student): |
| > | i2:=Int(x/sqrt(x^2+1),x=1..2); |
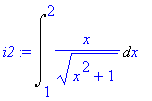
Zavedeme substituci
| > | changevar(t=x^2+1,i2,t); |
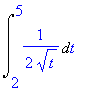
Snadno spočteme integrál
| > | value(%); |
![]()
| > |
| > |
Příklad 10
| > | restart:with(student): |
| > | i3:=Int(x*cos(x)^2,x=-Pi..Pi); |
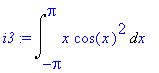
Všimněme si, že integrand je funkce lichá
| > | f:=unapply(integrand(i3),x); |
![]()
| > | is(f(-x)=-f(x)); # vlastnost liché funkce |
![]()
Tedy integrál roven 0
| > | value(i3); |
![]()
| > |
| > |
Příklad 11
| > | restart:with(student): |
| > | i4:=Int(x^3/(x^8+1),x=-1..0); |
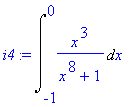
Zavedeme substituci a po dosazení vyměníme integrační meze
| > | changevar(x^4=u,i4,u); |
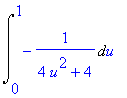
Integrál se snadno spočítá
| > | value(%); |
![]()
| > |
| > |
| > |
Integrály s proměnnými mezemi
Integrály s proměnnými mezemi využijeme později při výpočtu vícenásobných integrálů
| > | Int(x^2+1,x=1..y-1)=int(x^2+1,x=1..y-1); |
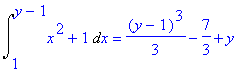
Následující příklad ukáže, že systém Maple se správně vyrovná i s kolizí označení, kdy proměnnou v horní mezi označíme stejným písmenkem x jako integrační proměnnou.
| > | Int(x^2+1,x=1..x-1); |
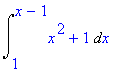
| > | value(%); |
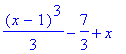
| > |
| > |
Nevlastní integrály
| > |
Příklad 12
| > | Int(1/sqrt(x-1),x=1..4); |
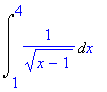
| > | value(%); |
![]()
Jedná se o nevlastní integrál. Integrand má singularitu v bodě 1.
| > |
Příklad 13
Určíme, zda dané integrály konvergují či divergují
| > | Int(1/x^3,x=1..infinity)=int(1/x^3,x=1..infinity); |
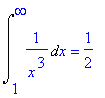
| > | Int(1/sqrt(x),x=1..infinity)=int(1/sqrt(x),x=1..infinity); |
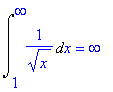
| > | Int(1/(x^2+1),x=-infinity..infinity)=int(1/(x^2+1),x=-infinity..infinity); |
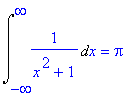
| > | Int(x/sqrt(x^5+1),x=0..infinity)=int(x/sqrt(x^5+1),x=0..infinity); |
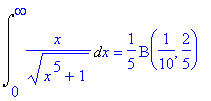
| > | Int((x^2+1)/(x^3+1),x=0..infinity)=int((x^2+1)/(x^3+1),x=0..infinity); |
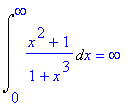
| > |
| > |
Příklad 14
| > | restart:with(student): |
| > | i:=Int(1/(1+x^3),x=0..infinity); |
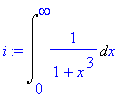
Rozložíme integrand na parciální zlomky. Pomocí příkazu integrand získáme integrand předchozího integrálu.
| > | iu:=convert(integrand(i),parfrac,x); |
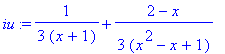
Spočteme primitivní funkci
| > | iu1:=int(iu,x); |
![]()
Dle Leibnitz-Newtonovy věty dosadíme meze. Pro infinity musíme počítat limitu.
| > | limit(iu1,x=infinity)-simplify(subs(x=0,%)); |
![]()
Kontrola výpočtu
| > | value(i); |
![]()
| > |
Příklad 15
| > | i:=Int(1/x,x=-1..1); |
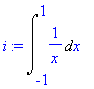
Problémem při integraci je neodstranitelná singularita v bodě 0. Proto rozdělíme integrál na dva a pokud oba konvergují, pak jejich součet je právě hledaným integrálem.
| > | i1:=Int(1/x,x=-1..0); |
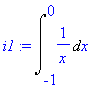
| > | i2:=Int(1/x,x=0..1); |
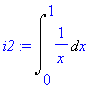
Spočítáme limitu pro x jdoucí k 0 z leva pro první z dílčích integrálů.
| > | limit(value(i1),x=0,left); |
![]()
Limita je nevlastní, a proto i původní integrál diverguje.
| > | value(i); |
![]()
| > |