Příklad 2

>    i2:=Int(1/sqrt(1-(sin(x))^4),x);

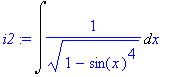
i2 := Int(1/((1-sin(x)^4)^(1/2)),x)

Vyjdeme ze vzorce [Maple OLE 2.0 Object]  , tj. [Maple OLE 2.0 Object] . Tedy označíme

>    i2p:=Int(1/((cos(x))^2*sqrt(1+2*(tan(x))^2)),x);

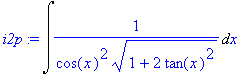
i2p := Int(1/(cos(x)^2*(1+2*tan(x)^2)^(1/2)),x)

a dostáváme

>    i2=i2p;

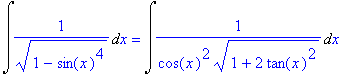
Int(1/((1-sin(x)^4)^(1/2)),x) = Int(1/(cos(x)^2*(1+2*tan(x)^2)^(1/2)),x)

Ze stejného důvodu jako v předcházejícím příkladu zavedeme substituci tg(x)=t .

>    i2p1:=changevar(t=tan(x),i2p); 

Error, (in changevar) usage: changevar(g(a) = f(b),F(..), b)

Je ohlášena chyba, neboť v relaci příkazu changevar  nová proměnná t  nevystupuje pouze na pravé straně. Chybu lze opravit takto: místo t=tan(x)  napíšeme  tan(x)=t , nebo do příkazu changevar  připíšeme třetí parametr, tím se vyhneme jakýmkoliv nepříjemnostem.

>    i2p1:=changevar(t=tan(x),i2p,t);  

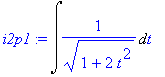
i2p1 := Int(1/((1+2*t^2)^(1/2)),t)

Tento integrál však ještě neumíme spočítat. Zavedeme v něm novou substituci [Maple OLE 2.0 Object] .

>    i2p2:=changevar(sqrt(2)*t=z,i2p1,z);

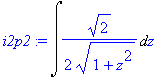
i2p2 := Int(1/2/(1+z^2)^(1/2)*2^(1/2),z)

Tento integrál již dovedeme spočítat

>    i2p3:=value(%);

i2p3 := 1/2*2^(1/2)*arcsinh(z)

Nyní se musíme vrátit zpět k původní proměnné, tj. dosadíme tan(x)=t  a [Maple OLE 2.0 Object]  , tj. [Maple OLE 2.0 Object]    

>    i2=subs(z=sqrt(2)*tan(x),i2p3);

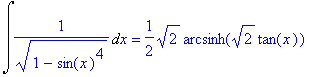
Int(1/((1-sin(x)^4)^(1/2)),x) = 1/2*2^(1/2)*arcsinh(2^(1/2)*tan(x))

Ještě poznamenejme, že systém Maple sám tento integrál takto elegantně nespočítá, posuďte sami.

>    value(i2);

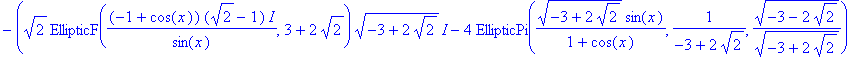
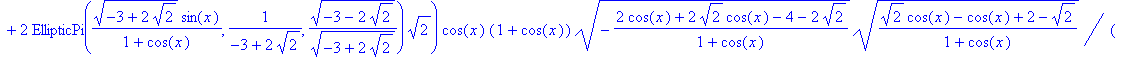
-(2^(1/2)*EllipticF((-1+cos(x))*(2^(1/2)-1)/sin(x)*I,3+2*2^(1/2))*(-3+2*2^(1/2))^(1/2)*I-4*EllipticPi((-3+2*2^(1/2))^(1/2)*sin(x)/(1+cos(x)),1/(-3+2*2^(1/2)),(-3-2*2^(1/2))^(1/2)/(-3+2*2^(1/2))^(1/2))+...
-(2^(1/2)*EllipticF((-1+cos(x))*(2^(1/2)-1)/sin(x)*I,3+2*2^(1/2))*(-3+2*2^(1/2))^(1/2)*I-4*EllipticPi((-3+2*2^(1/2))^(1/2)*sin(x)/(1+cos(x)),1/(-3+2*2^(1/2)),(-3-2*2^(1/2))^(1/2)/(-3+2*2^(1/2))^(1/2))+...
-(2^(1/2)*EllipticF((-1+cos(x))*(2^(1/2)-1)/sin(x)*I,3+2*2^(1/2))*(-3+2*2^(1/2))^(1/2)*I-4*EllipticPi((-3+2*2^(1/2))^(1/2)*sin(x)/(1+cos(x)),1/(-3+2*2^(1/2)),(-3-2*2^(1/2))^(1/2)/(-3+2*2^(1/2))^(1/2))+...

>