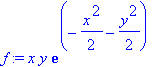| Extrémy funkce | |
|
Úvodní slovo Autor MAPLESystém MapleZáklady práce Konstrukce Maple Definice funkcí Zjednodušování Řešení rovnic Grafické zpracování Programování MatematikaDiferenciální počet Integrální početKřivkový integrál Plošný integrál Knihovnyplotsstudent Student VectorCalculus Knihovnyplotsstudent Student VectorCalculus InformaceDownloadOdkazy Publikace |
Systém Maple obsahuje příkazy pro výpočet extrémů jak volných tak i vázaných rovnicemi (nerovnicemi) a může velmi pomoci při řešení úloh hledání extrémů funkcí jedné nebo více proměnných.
Pro výpočet minimální hodnoty funkce jedné či více proměnných je určen příkaz minimize a pro nalezení maximální hodnoty příkaz maximize. Počítáme-li volné globální minimum (maximum) funkce, zadáme pouze funkci, tzn. příkazy mají jeden parametr. V případě omezení pomocí rovnic zadáme tato omezení jako další parametr. Pomocí intervalů lze také specifikovat oblast, ve které extrém hledáme. Oba příkazy vypíší hodnotu minima (maxima) dané funkce. Pomocí parametru location bude výpis rozšířen o souřadnice bodů, v nichž extrém nastává. Následující příklady ukáží použití těchto příkazů
> f:=x*y*exp(-(x^2+y^2)/2);
> maximize(%,location);
> minimize(%%,location);
> minimize(x^2-3*x+y^2*x+3,location);
> minimize(x^2-3*x+y^2*x+3,x=0..2,y=0..2,location);
> f1:=x^2-y^2+4;
> M:=x^2+y^2=1;
> maximize(f1,M);
> minimize(f1,M);
extrema(výraz, {omezení}, { proměnné }, ' souřadnice ') Poslední parametr je nepovinný, ale specifikuje řetězec, do kterého budou uloženy souřadnice bodů, v nichž nastává maximum a minimum. Tento příkaz nerozlišuje mezi minimy a maximy, hledá oba extrémy. Díky specifikaci proměnných můžeme tento příkaz užít také při hledání extrémů funkce s parametry, kdy pro některou hodnotu parametru nabývá funkce maxima a pro jinou minima. V případě hledání volného extrému, tj. nejsou žádné omezující podmínky, je nutné zadat druhý parametr v podobě prázdné množiny. Použití tohoto příkazu ukážeme na již zmíněném příkladu. Hledáme extrémy funkce
> f1;
> M;
> extrema(f1,{M},{x,y},'body');
> body;
|
| Ing. Vladimír Žák | |