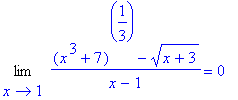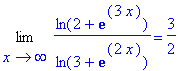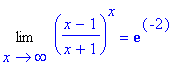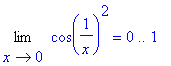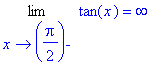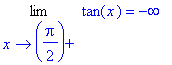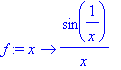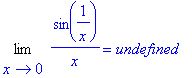| Limita funkce jedné proměnné | |
|
Úvodní slovo Autor MAPLESystém MapleZáklady práce Konstrukce Maple Definice funkcí Zjednodušování Řešení rovnic Grafické zpracování Programování MatematikaDiferenciální počet Integrální početKřivkový integrál Plošný integrál Knihovnyplotsstudent Student VectorCalculus Knihovnyplotsstudent Student VectorCalculus InformaceDownloadOdkazy Publikace |
Limita funkce je jedna ze základních a nejdůležitějších vlastností funkce. Příkaz, kterým se počítá limita funkce f(x) v bodě x=x0 má tvar
> Limit(((x^3+7)^(1/3)-sqrt(x+3))/(x-1),x=1)
> Limit(ln(2+exp(3*x))/ln(3+exp(2*x)),x=infinity)
> Limit(((x-1)/(x+1))^x,x=infinity)
> Limit(cos(1/x)^2,x=0)=limit(cos(1/x)^2,x=0);
> Limit(tan(x),x=Pi/2,left)=limit(tan(x),x=Pi/2,left);
> Limit(tan(x),x=Pi/2,right)
> Limit(tan(x),x=Pi/2)=limit(tan(x),x=Pi/2);
> f:=x->sin(1/x)/x;
> Limit(f(x),x=0)=limit(f(x),x=0);
|
| Ing. Vladimír Žák | |