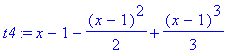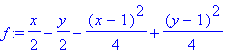|
Stažení mws souboru do Maple
Příkazy, pomocí kterých se v systému Maple počítá Taylorův rozvoj funkce f v okolí bodu
x = x0 , mají tvar
series( f(x),x=x0,n)
taylor( f(x),x=x0,n)
Místo funkce f(x) můžeme přímo uvést výraz pro výpočet hodnoty f(x). Stupeň n je nepovinným parametrem, který je implicitně nastaven na hodnotu 6 v proměnné Order (analogie s Digits ).
Dále systém Maple obsahuje příkaz pro potlačení zbytku, protože jinak by nešlo např. vykreslit daný rozvoj, popř. dosadit za proměnnou. Jde o příkaz
convert( taylor, polynom)
Pro snížení stupně Taylorova polynomu je v systému Maple k dispozici příkaz
rem(taylor, (x-x0)^n, x) , který odstraní všechny členy počínaje členem 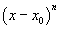 . .
Pro přímý výpočet Taylorova aproximačního polynomu se užívá příkaz
mtaylor( f(x),x=x0,n) , který se musel v předchozích verzích systému Maple nahrát do paměti pomocí příkazu readlib(mtaylor). Význam parametrů je shodný s předchozími příkazy.
V případě aproximace funkce dvou či více proměnných se užívají tyto příkazy v následujících tvarech
series( f(x,y), {x=x0,y=y0} ,n)
taylor( f(x,y), {x=x0,y=y0},n)
mtaylor( f(x,y), {x=x0,y=y0}, n)
Uveďme několik příkladů.
> t1:=series(cos(x),x=Pi);
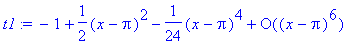
> Order;
# udává stupeň
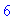
> Digits;
# udává počet platných desetinných míst
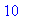
> t2:=taylor(sin(x),x=0,10);
# změna stupně aproximace
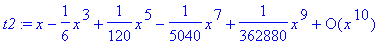
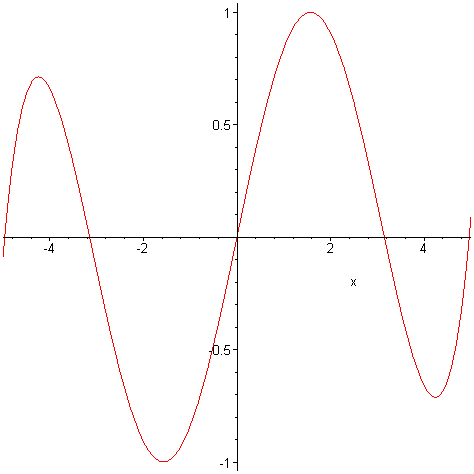
> plot(t2(x),x=-5..5);
# Maple neumí vykreslit kvůli zbytku O
Plotting error, empty plot
> t3:=convert(t2,polynom);
# odstranění zbytku
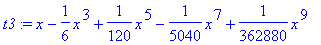
> plot(t3(x),x=-5..5);
> t4:=mtaylor(ln(x),x=1,4);
# přímý výpočet beze zbytku
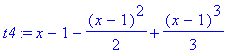
> rem(t4,x-1,x);
# odstranění již prvního členu
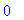
> rem(t4,(x-1)^2,x);
# odstranění všeho od zadaného členu
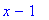
Funkce více proměnných
> f:=mtaylor((x-y)/(x+y),{x=1,y=1},3);
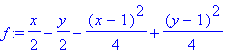
> f:=unapply(%,x,y);
# získáme funkci
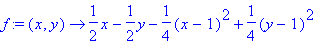
> f(1+h,1-k);
# výpočet hodnoty funkce v daném bodě
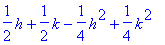
|