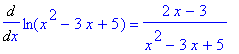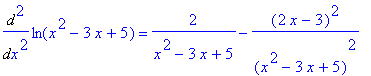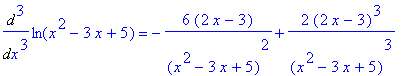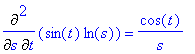Derivace funkce v systému Maple - Matematické výpočty v systému Maple

Derivace funkce

Dalším základním pojmem diferenciálního počtu je derivace funkce. K výpočtu první derivace funkce jedné proměnné jsou určeny příkazy

Diff( f(x), x) - matematický zápis
diff( f(x), x) - výpočet

Místo funkce f(x) lze v těchto příkazech použít i výraz pro výpočet hodnoty funkce. Pro určení hodnoty derivace funkce zapsané pomocí příkazu Diff lze užít příkaz value .

Pro výpočet druhé, popř. třetí, derivace funkce f(x) použijeme tento příkaz ve tvaru

diff( f(x),x,x) , popř.
diff( f(x),x,x,x) .

Vyšší stupeň derivace se tvoří přidáním dalšího parametru do příkazu diff .

> Diff(ln(x^2-3*x+5),x)=diff(ln(x^2-3*x+5),x);

> f:=x->ln(x^2-3*x+5);

> Diff(f(x),x,x)=diff(f(x),x,x);

> Diff(f(x),x$3)=diff(f(x),x$3);
# užití znaku $ jako opakovače - viz. posloupnosti

Příkaz diff lze také užít pro výpočet parciální derivace funkce více proměnných

diff( f(x,y,z), x) - parciální derivace podle proměnné x

> Diff(sin(t)*ln(s),t,s)=diff(sin(t)*ln(s),t,s);
# smíšená parciální derivace

Další možností, jak v Maplu vypočíst derivaci funkce, je operátor derivace D .

D(jméno funkce) - výpočet první derivace

( D@@n )(jméno funkce) - výpočet n -té derivace

Ekvivalentní zápis pomocí Diff je

Diff( jméno funkce, proměnná)

Pomocí operátoru derivace lze vypočíst derivace jak standardních funkcí, tak i funkcí definovaných uživatelem. Výsledkem provedení operace je opět funkce.

Operátor D je také obsažen v rozšiřující knihovně student . Proto další příklady užití tohoto operátoru naleznete v příloze student package .

> D(cos);