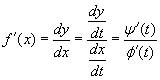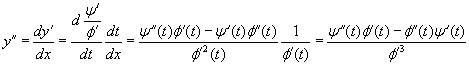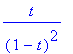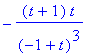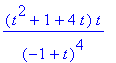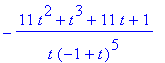Parametricky zadané funkce v systému Maple - Matematické výpočty v systému Maple

Parametricky zadané funkce

Tento odstavec ukáže možnost vytvoření vlastní procedury. Půjde o příkaz, pomocí kterého spočteme derivaci funkcí daných parametricky až do řádu čtyři včetně.

Nejprve uveďme několik vztahů, pomocí kterých se tyto derivace počítají.

Z věty o derivaci funkce dané parametricky má funkce f(x) v příslušném intervalu proměnné x derivaci a v odpovídajících si bodech platí .

Pro druhou derivaci platí

Pro třetí derivaci platí

Nyní přistupme k vytvoření již zmiňované procedury. Nazveme ji diffpar .

diffpar( [rce1,rce2], prom) - 1.derivace
diffpar( [rce1,rce2], prom, prom)          - 2. derivace
diffpar( [rce1,rce2], prom, prom, prom)    - 3. derivace
diffpar( [rce1,rce2], prom, prom, prom, prom)       - 4.derivace

Procedura diffpar

Tato procedura byla z důvodu přehlednosti napsána pomocí základních příkazů programování v systému Maple. Lze ji upravit tak, aby se chovala jako procedura, která je součástí programu. Jde především o typovou kontrolu. Pro pochopení je však nutné přečíst přílohu Programování - jazyk MPJ .

> diffpar:=proc(rce,prom)
  local vysl,x,y,dx,dy,dxx,dyy,dxxx,dyyy,dxxxx,dyyyy;

  if is(type(rce,'list')) and (nops(rce)=2) then 
     # spravny parametr
   else
     return  `Chyba - nespravny pocet rovnic`;
  end if; 

  x:=rce[1];             # získání zadaných rovnic 
  y:=rce[2];
  dx:=diff(x,prom);      # výpočet derivace
  dy:=diff(y,prom);
  
  if nargs=2 then
     lprint(`1.derivace`);
     vysl:=dy/dx ;
 
  elif nargs=3 then
     lprint(`2.derivace`);
     dxx:=diff(dx,prom);
     dyy:=diff(dy,prom);
     vysl:=simplify((dyy*dx-dxx*dy)/(dx)^3);    
 
  elif nargs=4 then 
     lprint(`3.derivace`);
     dxx:=diff(dx,prom);
     dyy:=diff(dy,prom);
     dxxx:=diff(dxx,prom);
     dyyy:=diff(dyy,prom);
     vysl:=simplify((dx^2*dyyy-dx*dy*
 	     dxxx-3*dx*dxx*dyy+3*dxx^2*dy)/(dx^5));

  elif nargs=5 then 
     lprint(`4.derivace`);
     dxx:=diff(dx,prom);
     dyy:=diff(dy,prom);
     dxxx:=diff(dxx,prom);
     dyyy:=diff(dyy,prom);
     dxxxx:=diff(dxxx,prom);
     dyyyy:=diff(dyyy,prom);
     vysl:=simplify(1/dx^5*(-6*dx^2*dxx*dyyy+
              dx^3*dyyyy-4*dx^2*dyy*dxxx-
              dx^2*dy*dxxxx+10*dx*dxx*dxxx*dy+
 		  15*dx*dxx^2*dyy-15*dxx^3*dy));
 
  elif nargs>5 then
     return `Tato procedura pocita max. 4.derivaci`;
  end if;   
 
 return vysl;
 end proc:

Ukázka použití

> diffpar([ln(t),1/(1-t)],t);

`1.derivace`