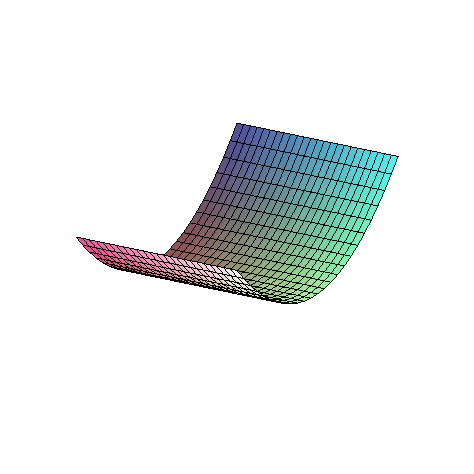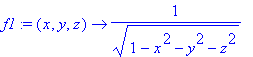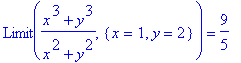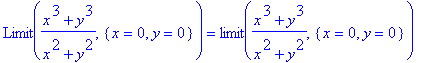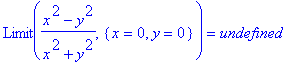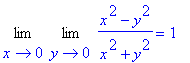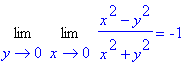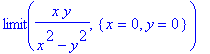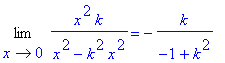Limita funkce více proměnných v systému Maple - Matematické výpočty v systému Maple

Limita funkce více proměnných

Nejprve zopakujme práci s funkcemi více proměnných v systému Maple.

> f:=(x,y)->x^2+y;
# definice funkce dvou proměnných

> plot3d(f,-2..2,-2..2);
# nakreslení grafu

> f1:=(x,y,z)->1/sqrt(1-x^2-y^2-z^2);

> singular(f1(x,y,z),{x,y,z});
# body nespojitosti, více viz. spojitost funkce

Výpočet limity funkce více proměnných je obecně velmi problematická. Výpočet limity funkce dvou proměnných se provádí pomocí příkazu

limit( f(x,y),{x=x0,y=x0})

Vše, co bylo v předchozím odstavci řečeno o příkazu limit , platí i zde.

Pro výpočet dvojnásobné limity užijeme konstrukce

limit(limit(f(x,y),x=x0),y=y0)

Uveďme několik příkladů.

> Limit((x^3+y^3)/(x^2+y^2),{x=1,y=2})
=limit((x^3+y^3)/(x^2+y^2),{x=1,y=2});
# Maple limitu spočítá

> Limit((x^3+y^3)/(x^2+y^2),{x=0,y=0})
=limit((x^3+y^3)/(x^2+y^2),{x=0,y=0});
# Maple neumí limitu spočítat

Následující příklad ukazuje využití dvojnásobných limit při důkazu neexistence limity

> Limit((x^2-y^2)/(x^2+y^2),{x=0,y=0})
=limit((x^2-y^2)/(x^2+y^2),{x=0,y=0});

> Limit(Limit((x^2-y^2)/(x^2+y^2),y=0),x=0)
=limit(limit((x^2-y^2)/(x^2+y^2),y=0),x=0);

> Limit(Limit((x^2-y^2)/(x^2+y^2),x=0),y=0)
=limit(limit((x^2-y^2)/(x^2+y^2),x=0),y=0);

Další příklad ukazuje, že rovnost dvojnásobných limit nezaručuje existenci limity

> limit(x*y/(x^2-y^2),{x=0,y=0});

> limit(limit(x*y/(x^2-y^2),x=0),y=0);

> limit(limit(x*y/(x^2-y^2),y=0),x=0);

Nyní se k počátku soustavy souřadnic budeme blížit po přímkách

> y:=k*x;

> Limit(x*y/(x^2-y^2),x=0)=limit(x*y/(x^2-y^2),x=0);

Vidíme, že výsledná limita je závislá na volbě konstanty k , proto limita původní funkce neexistuje.

Ing. Vladimír Žák

MAPLE

Matematika

Knihovny

Knihovny

Informace