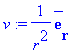| VectorField - knihovna VectorCalculus | |
|
Úvodní slovo Autor MAPLESystém MapleZáklady práce Konstrukce Maple Definice funkcí Zjednodušování Řešení rovnic Grafické zpracování Programování MatematikaDiferenciální početIntegrální počet Křivkový integrál Plošný integrál Knihovnyplotsstudent Student VectorCalculus InformaceDownloadOdkazy Publikace |
VectorField
> with(VectorCalculus); [&x, *, +, -, ., <,>, <|>, AddCoordinates, ArcLength, BasisFormat, Binormal, CrossProd, CrossProduct, Curl, Curvature, D, Del, DirectionalDiff, Divergence, DotProd, DotProduct, Flux, GetCoordinateParameters, GetCoordinates, Gradient, Hessian, Jacobian, Laplacian, LineInt, MapToBasis, Nabla, Norm, Normalize, PathInt, PrincipalNormal, RadiusOfCurvature, ScalarPotential, SetCoordinateParameters, SetCoordinates, SurfaceInt, TNBFrame, Tangent, TangentLine, TangentPlane, TangentVector, Torsion, Vector, VectorField, VectorPotential, Wronskian, diff, evalVF, int, limit, series] > v := VectorField( <x,y,z>, 'cartesian'[x,y,z] );# Vektorové pole v kartézské soustavě souřadnic
# Zjištění vlastností objektu v
# Vektorové pole zadané ve sférických souřadnicích
# Zjištění vlastností objektu v
# Vyčíslení hodnoty vektorového pole v daném bodě, pomocí simplify bylo provedeno pouze zjednodušení. Vektor v je ve sférických souřadnicích a bod je zadán v kartézské soustavě souřadnicové.
# Změna pracovních souřadnic na cylindrické
# Vektorové pole zadané v těchto souřadnicích
# Zjištění vlastností
|
| Ing. Vladimír Žák | |