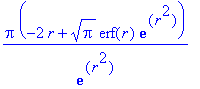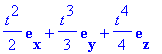Výpočet integrálu pomocí tohoto příkazu předpokládá vyjádření oblasti pomocí předem předepsaných forem, jinak se tento postup nedá užít.

Syntaxe:

int(fce, dom)    , kde fce je výraz, který představuje integrand, a parametr dom určuje oblast integrace.

Oblast je vyjádřena pomocí jedné z následujících možností:

• Circle(cen, rad),
• Ellipse(eqn),
• Parallelepiped(r1, [r2, r3, ..]),
• Rectangle(r1, r2),
• Region(r1, [r2, r3, ...]),
• Sector(obj, start, finish),
• Sphere(cen, rad),
• Tetrahedron(v1, v2, v3, v4),
• Triangle(v1, v2, v3).

Více podrobností o jednotlivých vyjádřeních naleznete v nápovědě, například pomocí příkazu ?VectorCalculus[int].

> with(VectorCalculus);

[&x, *, +, -, ., <,>, <|>, AddCoordinates, ArcLength, BasisFormat, Binormal, CrossProd, CrossProduct, Curl, Curvature, D, Del, DirectionalDiff, Divergence, DotProd, DotProduct, Flux, GetCoordinateParameters, GetCoordinates, Gradient, Hessian, Jacobian, Laplacian, LineInt, MapToBasis, Nabla, Norm, Normalize, PathInt, PrincipalNormal, RadiusOfCurvature, ScalarPotential, SetCoordinateParameters, SetCoordinates, SurfaceInt, TNBFrame, Tangent, TangentLine, TangentPlane, TangentVector, Torsion, Vector, VectorField, VectorPotential, Wronskian, diff, evalVF, int, limit, series]

Přejděte zpět na:

• stránku o knihovně VectorCalculus