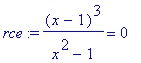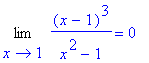Po použití příkazu solve se doporučuje provést zkoušku. Následující příklad ukáže nutnost tohoto kroku. Nalezněme tedy řešení rovnice

Řešení budeme hledat užitím příkazu solve v následujícím tvaru

Systém Maple nalezl řešení, ale tato rovnice řešení nemá. Důvodem je odstranitelná singularita zlomku v bodě x= 1. Ukažme, že jde o odstranitelnou singularitu a tedy právo dodefinovat hodnotu v tomto bodě.

Spočtěme tedy limitu

Vidíme, že systém Maple odstranil singularitu v bodě x =1 ještě před řešením dané rovnice. A to je důvodem k provádění zkoušky po použití příkazu solve .

Na dalším příkladu si ukážeme, jak efektivně provést dosazení výsledků do původní rovnice. Pro tuto operaci lze použít příkaz subs .
Příkaz
      subs(co, kam);
provádí obecně substituce v Maple.

Vraťme se ke kontrole výsledků pomocí příkazu subs . Řešme soustavu rovnic

Nyní provedeme zkoušku dosazením výsledků do soustavy rovnic

Bylo nutné užít indexového zápisu, protože řešením dané soustavy rovnic v Maplu jsou dvě množiny, které z pochopitelných důvodů musíme dosazovat postupně, tj. přistupujeme k nim pomocí již zmíněného indexového zápisu.

Poznámka:
V této chvíli je nutné poznamenat, že si novější verze systému Maple mohou již s tímto příkladem poradit, nicméně i tak je tento konkrétní příklad ukázkou nutnosti provádění zkoušky.