| Numerické řešení algebraických rovnic - fsolve | |
|
Úvodní slovo Autor MAPLESystém MapleZáklady práce Konstrukce Maple Definice funkcí Zjednodušování Řešení rovnic
Programování MatematikaDiferenciální početIntegrální počet Křivkový integrál Plošný integrál Knihovnyplotsstudent Student VectorCalculus InformaceDownloadOdkazy Publikace |
Systém Maple také nabízí možnost numerického řešení pomocí příkazu fsolve . Použití a volání je analogické s příkazem solve . > solve({x^4-6*x^2-3*x-5},{x}); # řešení symbolicky
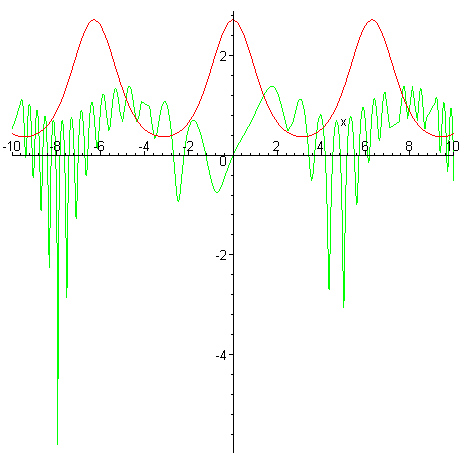
V případě, že Maple neumí nalézt řešení symbolicky, nevypíše žádný výsledek. To samozřejmě neznamená, že řešení neexistuje. Ukažme si to na příkladu. > solve({exp(cos(x))=ln(2+sin(x)-cos(x^2))},{x});# symbolické řešení neumí nalézt > Maple neumí řešení symbolicky nalézt. Následující obrázek ukazuje, že řešení existuje. Proto užijeme příkazu fsolve pro numerické řešení. > pl1:=plot(exp(cos(x)),x=-10..10):# vykreslení grafů funkcí pl2:=plot(ln(2+sin(x)-cos(x^2)), x=-10..10,color=green): > plots[display]({pl1,pl2});
# numerické řešení
V případě, že chceme, aby Maple vypsal numerické řešení v zadaném intervalu, můžeme tento interval určit pomocí třetího parametru > fsolve({exp(cos(x))=ln(2+sin(x)-cos(x^2))},{x},0..3);# numerické řešení na <0,3>
V případě, že numerické řešení na daném intervalu nelze nalézt, je vypsán zadaný příkaz > fsolve({exp(cos(x))=ln(2+sin(x)-cos(x^2))},{x},-1..1);# numerické řešení na <-1,1>
|
| Ing. Vladimír Žák | |