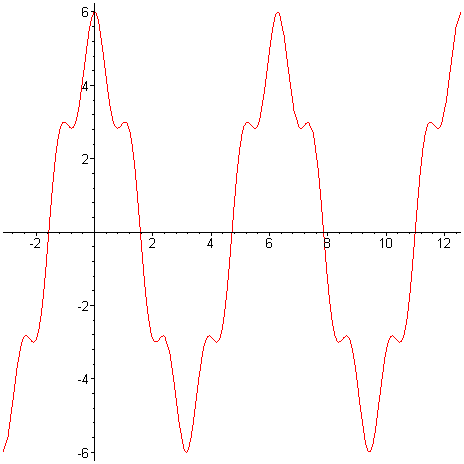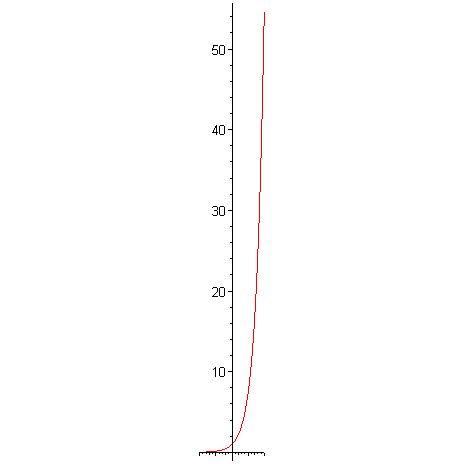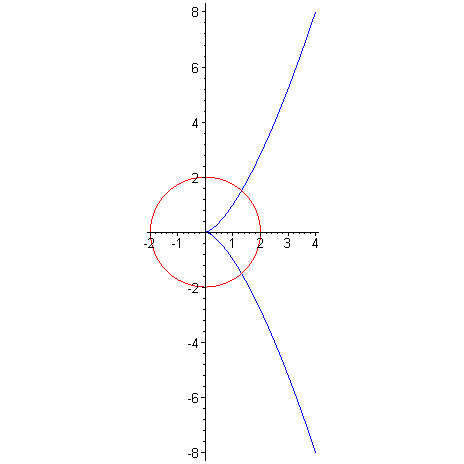Základy grafického zpracování ve 2D

Jak již bylo řečeno, nejjednodušším příkazem je příkaz plot.

plot(výraz, proměnná = a..b);
plot(funkce, a..b);
plot(funkce, a..b,c..d);

První příkaz vykreslí daný výraz (jde o předpis funkce) na daném intervalu. Druhý se používá pro vykreslení funkce f(x) na daném intervalu a třetí vykresluje funkce na kartézském čtverci .

> plot(cos(x)/x,x=0..infinity);
# vykreslení grafu funkce dané výrazem

> f:=x->5*cos(x)+cos(5*x):
> plot(f,-Pi..4*Pi); # vykreslení grafu funkce
plot(f(x),x=-Pi..4*Pi):
# ekvivalentní zápis pomocí výrazu

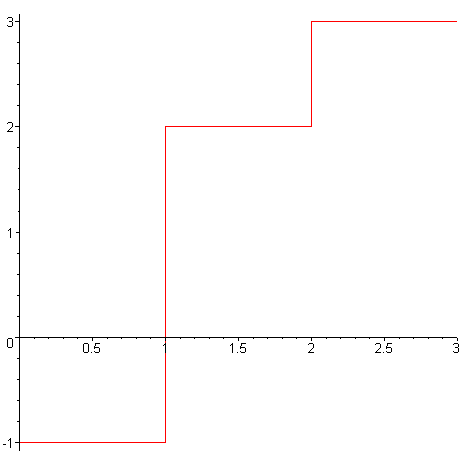
Systém Maple kreslí grafy funkcí jako spojitou křivku, což v konečném důsledku může znehodnotit graf funkce dané po částech. Vysvětlení ukážeme na následujícím příkladu.

> f1:=x->piecewise(x<1,-1,x<2,2,3);
# funkce daná po částech

> plot(f1,0..3); # vykreslení funkce

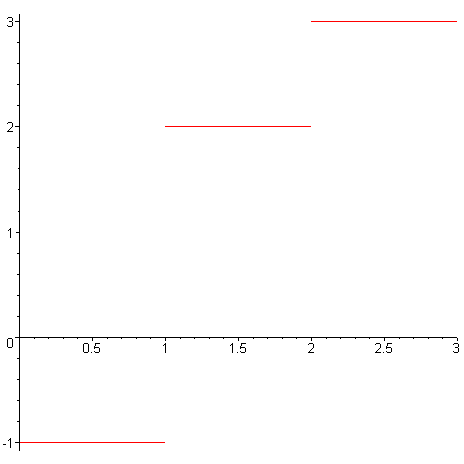
Předchozí obrázek nelze považovat za graf funkce kvůli svislým úsečkám. Je nutné tyto úsečky odstranit, tzn. povolit nespojitosti. Toho docílíme přidáním třetího parametru do příkazu plot , a to discont=true/false. Hodnota false je implicitní.

> plot(f1,0..3,discont=true); # povolení nespojitostí

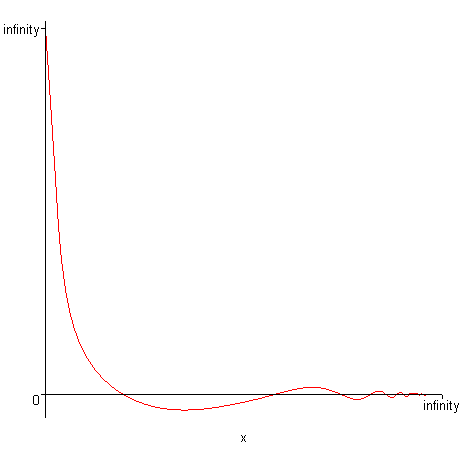
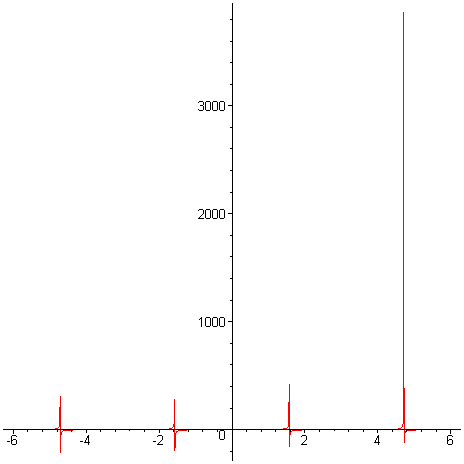
Další příklad shrne dosavadní poznatky o zobrazování funkcí. Nakresleme funkci tangens.

> plot(tan,-2*Pi..2*Pi); # funkce tangens

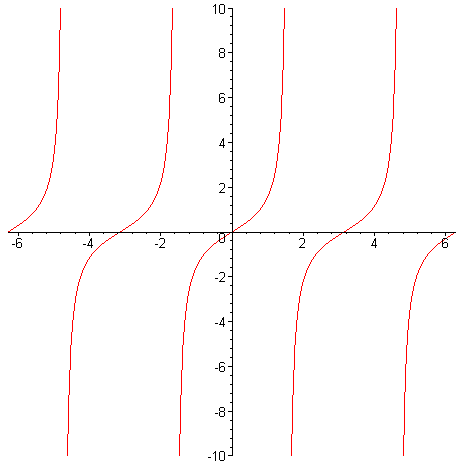
Předchozí obrázek nepřipomíná graf funkce tangens, ale opravdu je jejím grafem. Problémem je, že měřítko na ose y je velmi malé. K odstranění problému využijeme třetí možnou syntaxi příkazu plot .

> plot(tan,-2*Pi..2*Pi,-10..10);
# omezení hodnot na ose y

Při použití parametru discont dostaneme.

> plot(tan,-2*Pi..2*Pi,-10..10, discont=true);

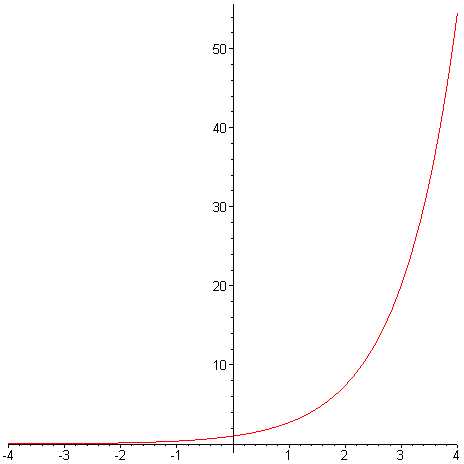
Systém Maple implicitně nevykresluje souřadnicové osy ve stejném měřítku, a tím někdy dochází ke zkreslení informace o průběhu funkce. Pro vykreslení stejného měřítka na obou osách je určen parametr scaling = constrained / unconstrained Hodnota unconstrained je implicitní.
Následující dva obrázky zdůrazní důležitost tohoto parametru.

> plot(exp,-4..4);

> plot(exp,-4..4,scaling=constrained);

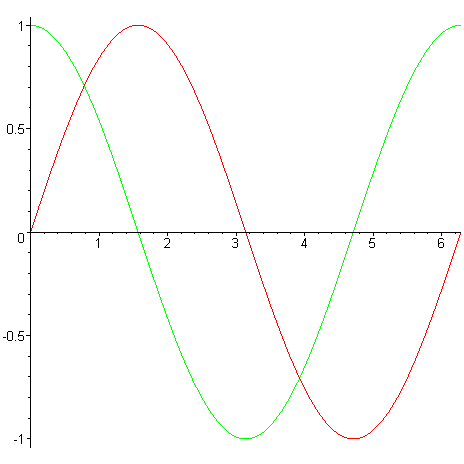
Maple samozřejmě umožňuje vykreslit více grafů do jednoho obrázku, a to pomocí konstrukce

plot( [seznam funkcí], proměnná = rozsah );

Zde je nutné zdůraznit, že jde o seznam. Je tedy nutné použít [.].

> plot([sin,cos],0..2*Pi); # vykreslení funkci sin, cos

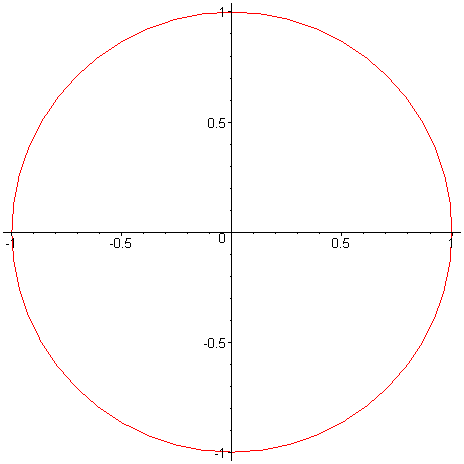
Velmi podobný způsob zápisu se užívá u funkcí zadaných parametrickými rovnicemi. Zde jde o konstrukci

plot( [ relace1,relace2 , proměnná = rozsah ] );

Rozdíl je v použití hranatých závorek.

> plot([sin,cos,0..2*Pi]);
# parametrické zadání kružnice

Pro vykreslení více funkcí zadaných parametrickými rovnicemi je nutné zdvojit [.].

> plot([[2*cos(t),2*sin(t),t=0..2*Pi] ,
[s^2,s^3,s=-2..2] ],
scaling=constrained, color=[red, blue]);

Příkaz plot má mnoho dalších parametrů. Uveďme nejčastěji používané

color = [barva1,barva2, ...]
- definice barev funkcí dle pořadí jejich zadání (lze užít i konstrukci RGB)
linestyle = [hodnota, hodnota, ...]
- definice stylu čar ( každý styl má přiřazenou určitou hodnotu, viz. HELP)
title = `řetězec`
- nadpis grafu
legend = [`křivka1`,`křivka2`, ...]
- definice legendy
labels = [`osa x`, `osa y`, ...]
- pojmenování souřadnicových os

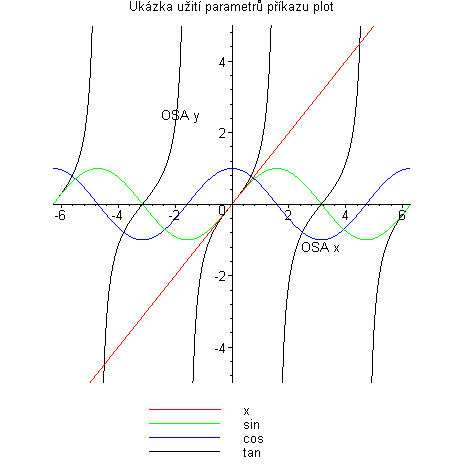
Ještě poznamenejme, že většinu parametrů příkazu plot lze nastavit z kontextového menu vybráním příslušné položky.

> fce:=[x,sin(x),cos(x),tan(x)]:
> plot(fce,
    x= -2*Pi..2*Pi,    # definiční obor
    -5..5,             # obor hodnot na ose y
    color=[red, green, blue, black],
       # definice barev
    title=`Ukázka užití parametrů příkazu plot`,
       # titulek obrázku
    discont=true,      # povoleny singularity
    legend=[`x`,`sin`,`cos`,`tan`],
       # definice legendy
    labels=[`OSA x`,`OSA y`]
       # pojmenování souřadnicových os
);

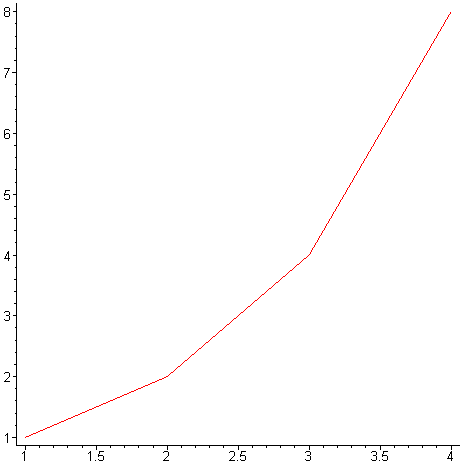
Ještě se krátce zastavme u vykreslování bodů. Jednotlivé body uzavřeme jako seznam do [.].

> body:=[[1,1],[2,2],[3,4],[4,8]];

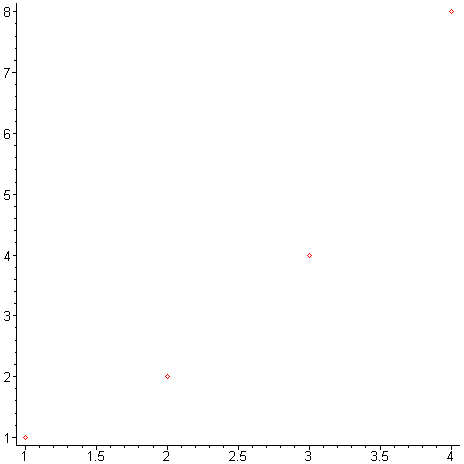
> plot(body); # implicitně kreslí spojitou křivku

Pro vykreslení pouze jednotlivých bodů musíme užít parametru style = point .

> plot(body,style=point); # zobrazení pouze bodů

Ing. Vladimír Žák

MAPLE

Matematika

Knihovny

Informace