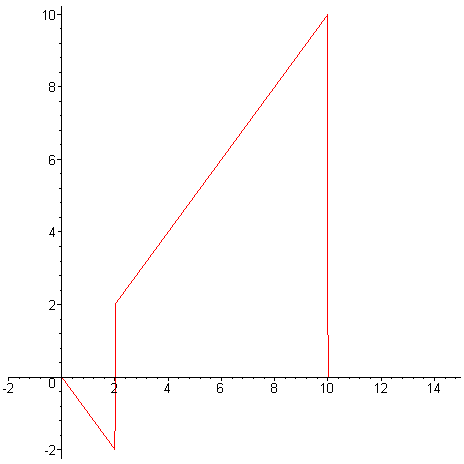Existují však funkce, které bychom tímto způsobem jen těžko definovali. Jde o funkce, které jsou definovány po částech. Ukažme si to na jednoduchém příkladu. Mějme funkci definovanou po částech:

Tato funkce nemůže být zapsána pomocí předchozích předpisů. Musíme tedy využít jiného zápisu, tedy pomocí klíčového slova piecewise .

jmeno_fce := (prom_1,…,prom_n) ->piecewise(nerovnost_1,hodnota_1,…,…,
                       nerovnost_n,hodnota_n);

Zapišme výše uvedenou funkci danou po částech

Všimněte si, že poslednímu parametru (tedy 0) není určen interval, to tedy znamená, že zastupuje hodnotu funkce v nedefinovaných intervalech.

Za nejobecnější definici funkce (používá se při programovaní v Maplu) však bývá často považována definice pomocí klíčového slova proc .

jmeno_fce := proc(prom_1,…,prom_n) tělo funkce end proc;

V tomto případě lze v definici funkce využít programovacího jazyka zabudovaného v Maplu.