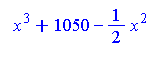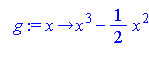AntiderivatePlot
Tento příkaz je určen pro zobrazení funkce a jí příslušné primitivní funkce na daném intervalu a to včetně aditivní konstanty, která je vypočtena vzhledem k levému krajnímu bodu daného intervalu. Tento bod lze změnit pomocí parametru value. Příkaz má několik dalších nepovinných parametrů, které jsou však velmi dobře vysvětleny v nápovědě systému Maple. Uveďme několik příkladů.

Hledejme primitivní funkci k funkci

> with(Student[Calculus1]):
> f := x -> 3*x^2 - x;

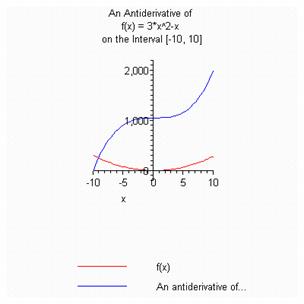
Nejprve ukažme nalezení primitivní funkce na implicitním intervalu Parametr output v následujícím příkazu určuje, že výstupem nebude graf.
> AntiderivativePlot(f(x), output = antiderivative);

Výsledek prvního příklad se může zdát zvláštní. Jak systém Maple přišel na konstantu 1050? Implicitní interval pro hledání implicitní funkce je nastaven na <-10,10>. Nyní se podívejme, jak systém Maple dospěl dané konstantě. Hledáme tvar primitivní funkce, která splňuje podmínku F(a)=0, kde a je levým krajním bodem zadaného intervalu. V našem případě jde o bod se souřadnicí x=-10. Funkce g je primitivní funkcí k zadané funkci.

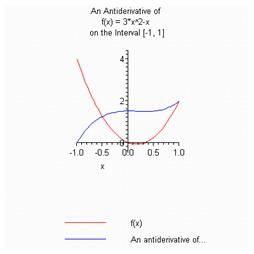
Nyní již víme, jakým způsobem je aditivní konstanta počítána. Následující příklady ukazují další možná použití tohoto příkazu. Změna intervalu se provádí pomocí zadaní intervalu pro neznámou x.
> AntiderivativePlot(f(x), x = 0..1, output = antiderivative);

Pro výpočet aditivní konstanty lze zadat bod, ve kterém má být splněna výše uvedená podmínka. Zadává se pomocí parametru value.
> AntiderivativePlot(f(x), output = antiderivative, value = [0,0]);

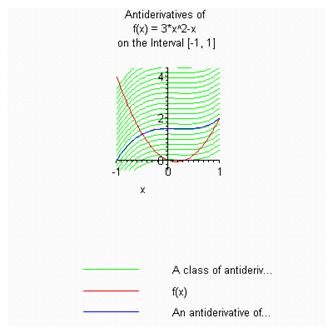
Následující příklad ukazuje, jak lze vykreslit primitivní funkce k dané funkci pomocí parametru showclass.
> AntiderivativePlot(f(x), -1..1, value = 0, showclass);

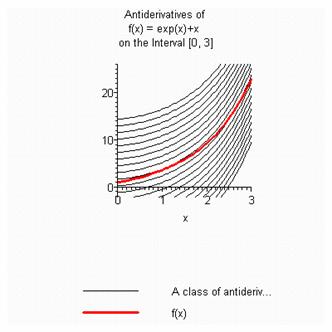
Poslední příklad ukazuje další možná ovlivnění grafického výstupu.
> AntiderivativePlot(exp(x) + x, x=0..3, showclass,
  showantiderivative=false,
  functionoptions=[thickness=2],
  classoptions=[color=black]);

Přejděte zpět na:

• seznam příkazů pro vizualizaci
• Student[Calculus1]