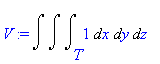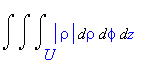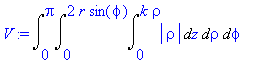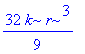Dvojný integrál a jeho aplikace
Nyní uveďme několik příkladů.
Příklad 1
Vypočítejte dvojný integrál přes obdélník zadaný nerovnostmi 0<=x<=2, 0<=y<=1
| > | restart:with(student): |
| > | Doubleint(x^2+y^2,x=0..2,y=0..1); |
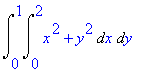
| > | value(%); |
![]()
| > |
| > |
Příklad 2
Vypočítejte dvojný integrál přes oblast M
| > | restart:with(student):with(plots): |
Warning, the name changecoords has been redefined
Zadaný integrál
| > | i2:=Doubleint(x^2+y^2,x,y,M); |
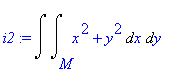
M je množina mezi dvěma křivkami
| > | M:={y^2=2*x,y=x-4}; |
![]()
Nakreslíme oblast M
| > | p1:=implicitplot(M[1],x=-1..10,y=-3..6): |
| > | p2:=plot(rhs(M[2]),x=-1..10,y=-3..6): # pomocí rhs získáme pravou stranu rovnice |
| > | display({p1,p2}); |
![[Maple Plot]](image/dvojnytrojny_komplet5.gif)
Nalezneme průsečíky křivek pomocí příkazu intercept
| > | intercept(M[1],M[2],{x,y}); |
![]()
Výhodnější je integrovat nejprve dle x a pak dle y .
Pro získání mezí pro x použijeme příkaz isolate , který vyjádří danou proměnnou z rovnice.
| > | omez:={y=-2..4,x=rhs(isolate(M[1],x))..rhs(isolate(M[2],x))}; |
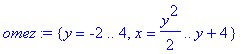
Počítáme tedy integrál
| > | i2u:=Doubleint(x^2+y^2,omez[2],omez[1]); |
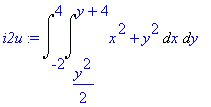
Všimněte si, že pokud zadáme meze v opačném pořadí, změní se i pořadí integrace.
Vždy je nutné mít konstantní meze při poslední integraci! Ukažme to následujícími dvěma příkazy.
| > | _i2u:=Doubleint(x^2+y^2,omez[1],omez[2]); |
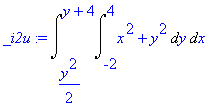
Výpočet integrálu
| > | value(_i2u); |
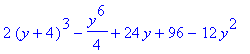
Spočítejme výslednou hodnotu, ze správně zadaného dvojného integrálu
| > | value(i2u); |
![]()
| > |
| > |
Příklad 3
| > | restart:with(student):with(plots): |
Warning, the name changecoords has been redefined
Vypočítejte dvojný integrál přes trojúhelník daný 3 body
| > | i3:=Doubleint(x*y,x,y,M); |
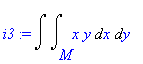
| > | M:={[0,0],[1,1],[2,0]}; |
![]()
Nakreslíme oblast M
| > | polygonplot(M); |
![[Maple Plot]](image/dvojnytrojny_komplet14.gif)
Pro lepší zobrazení integrační oblasti užijeme příkaz inequal , kde prvním parametrem je množina rovnic přímek, které procházejí danými body.
| > | inequal({x>=y,x<=2-y},x=-0..2,y=0..2,optionsfeasible=(color =blue), optionsexcluded=(color=gray),optionsclosed=(color=yellow),thickness=2); |
![[Maple Plot]](image/dvojnytrojny_komplet15.gif)
Určíme meze integrace
| > | omez:=x=y..2-y,y=0..1; |
![]()
Počítáme tedy integrál
| > | i3u:=Doubleint(x*y,omez); |
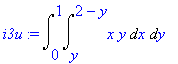
Spočítáme výslednou hodnotu
| > | value(i3u); |
![]()
| > |
Příklad 4
Tento příklad ukazuje důležitost volby pořadí integrace
| > | restart:with(student):with(plots): |
Warning, the name changecoords has been redefined
Vypočítejme dvojný integrál přes zadanou oblast M
| > | Doubleint(sin(y^2),x,y,M); |
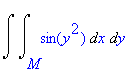
| > | M:=x=0,y=x,y=Pi; |
![]()
Nakreslíme oblast integrace M .
| > | inequal({x>=0,y>=x,y<=Pi},x=-0..4,y=0..4,optionsfeasible=(color =blue), optionsexcluded=(color=gray),optionsclosed=(color=yellow),thickness=2); |
![[Maple Plot]](image/dvojnytrojny_komplet21.gif)
Počítáme tedy integrál
| > | i4:=Doubleint(sin(y^2),y=rhs(M[2])..Pi,x=0..Pi); |
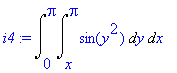
Tento integrál neumíme jednoduše vypočítat, protože
![]() neumíme vyjádřit pomocí elementárních funkcí
neumíme vyjádřit pomocí elementárních funkcí
Výsledkem je
| > | value(%); |
![1/2*FresnelS(2^(1/2)*Pi^(1/2))*2^(1/2)*Pi^(3/2)-1/12*Pi^4*hypergeom([3/4, 1],[3/2, 7/4, 2],-1/4*Pi^4)](image/dvojnytrojny_komplet24.gif)
Nyní zaměníme pořadí integrace. Nejprve budeme integrovat dle x .
| > | i4u:=Doubleint(sin(y^2),x=0..lhs(M[2]),y=0..Pi); |
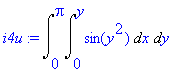
Tento integrál snadno spočítáme
| > | value(%); |
![]()
Jak je z tohoto příkladu vidět, volba pořadí integrace je velmi důležitá.
| > |
Substituce
ve dvojném integrálu se provádí pomocí příkazu
changevar( {relace} , Doubleint( f(x,y) , x, y, oblast), [nové proměnné])
relace uvádí vztah mezi původními a novými proměnnými. V případě jednoduchého integrálu byly transformovány i meze integrace. V případě vícenásobných integrálů nejsou meze integrace transformovány!
| > |
Příklad 5
Počítejme dvojný integrál přes čtvrtkruh o poloměru r v I. kvadrantu.
| > | restart:with(student):with(plots): |
Warning, the name changecoords has been redefined
| > | i5:=Doubleint(sqrt(x^2+y^2),x,y,M); |
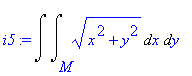
Vykreslíme oblast pro r = 1
| > | implicitplot(x^2+y^2=1,x=0..1,y=0..1); # vykreslí funkci danou implicitně |
![[Maple Plot]](image/dvojnytrojny_komplet28.gif)
Použijeme substituci do polárních souřadnic. Oblast M v kartézských souřadnicích přejde po substituci v oblast N v polárních souřadnicích.
| > | i5u:=changevar({x=u*cos(v),y=u*sin(v)},subs(M=N,i5),[u,v]); |
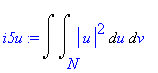
Jak již bylo řečeno, příkaz changevar v tomto případě neprovede transformaci mezí. Transformaci provedeme sami. Jde o čtvrtkruh, tzn. že pro nové proměnné platí 0<= u <= r , 0<= v <= Pi/2.
Tedy počítáme integrál
| > | Doubleint(integrand(i5u),u=0..r,v=0..Pi/2); |
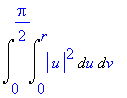
Výsledkem výpočtu je
| > | value(%); |
![]()
| > |
| > |
Příklad 6
| > | restart:with(student):with(plots): |
Warning, the name changecoords has been redefined
Počítejme integrál přes oblast A .
| > | i6:=Doubleint(1,x,y,A); |
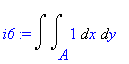
Oblast A je omezena křivkami zadanými rovnicemi
| > | omez:=[x^2+y^2=x,x^2+y^2=2*x,y=x,y=sqrt(3)*x]; |
![]()
Pro názornost oblast nakreslíme
| > | p1:=implicitplot(omez[1],x=-1..2,y=-1..2,numpoints=5000): |
| > | p2:=implicitplot(omez[2],x=-1..2,y=-1..2,numpoints=5000): |
| > | p3:=plot(rhs(omez[3]),x=-1..2,y=-1..2): |
| > | p4:=plot(rhs(omez[4]),x=-1..2,y=-1..2): p5:=textplot([0.5,0.70,"A"],align={ABOVE,RIGHT},color=blue, font=[TIMES,BOLD,20]): |
| > | display({p1,p2,p3,p4,p5}); |
![[Maple Plot]](image/dvojnytrojny_komplet34.gif)
Použijeme substituci do polárních souřadnic. Oblast A v kartézských souřadnicích po substituci přejde v oblast B v polárních souřadnicích. Proto bylo použito příkazu subs .
| > | s:=x=u*cos(v),y=u*sin(v); |
![]()
| > | i6u:=changevar({s},subs(A=B,i6),[u,v]); |
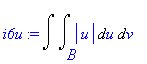
Je třeba transformovat meze. Dosadíme rovnice transformace do rovnic křivek
| > | o1:=simplify(subs(s,omez[1])); |
![]()
| > | o2:=simplify(subs(s,omez[2])); |
![]()
Dále z rovnic přímek získáme informace o úhlu pomocí směrnice
| > | o3:=solve(tan(x)=1,x); |
![]()
| > | o4:=solve(tan(x)=sqrt(3),x); |
![]()
Počítáme tedy integrál (protože jsme dále neupravovali meze, sami vykrátíme u v o1 a o2 )
| > | i6p:=Doubleint(u,u=rhs(o1)/u..rhs(o2)/u,v=o3..o4); |
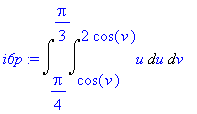
Výsledek spočítáme pomocí
| > | value(i6p); |
![]()
| > |
Příklad 7
| > | restart:with(student):with(plots): |
Warning, the name changecoords has been redefined
Počítejte obsah elipsy
| > | el:=(x/a)^2+(y/b)^2<=1; assume(a>0,b>0): |
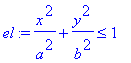
Nakreslíme obrázek pro pevně zvolené parametry a=3, b=2
| > | implicitplot((x/3)^2+(y/2)^2=1,x=-3..3,y=-3..3,scaling=constrained,numpoints=5000); |
![[Maple Plot]](image/dvojnytrojny_komplet44.gif)
Zavedeme zobecněné polární souřadnice
| > | s:=x=a*u*cos(v),y=b*u*sin(v); |
![]()
Určíme meze pro novou proměnnou u dosazením do rovnice elipsy
| > | simplify(subs(s,el)); |
![]()
Integrační meze pro v , 0<=v<=2*Pi . Po provedení substituce a dosazením mezí dostáváme
| > | changevar({s},Doubleint(1,x,y,M),[u,v]); |
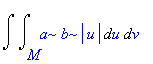
| > | i7:=Doubleint(integrand(%),u=0..1,v=0..2*Pi); |
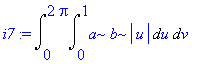
Obsah elipsy je roven
| > | value(i7); |
![]()
| > |
Příklad 8
Vypočtěte integrál
| > | restart:with(student):with(plots): |
Warning, the name changecoords has been redefined
| > | i8:=Doubleint(x,x,y,M); |
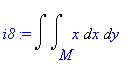
kde M je kruh
| > | kruh:=x^2+y^2<=2*r*x; assume(r>0); |
![]()
Tento dvojný integrál spočteme v polárních souřadnicích.
Kruh M má střed na ose x a dotýká se y v počátku, což plyne z dané nerovnice doplněním na součet úplných čtverců.
| > | completesquare(x^2+y^2-2*r*x<=0,x); # doplnění na součet úplných čtverců |
![]()
Nakreslíme oblast M pro pevně zvolené r=1
| > | implicitplot(x^2+y^2=2*x,x=-1..2,y=-1..1,numpoints=600); |
![[Maple Plot]](image/dvojnytrojny_komplet53.gif)
Zavedeme polární souřadnice. Oblasti M zadané v kartézských souřadnicích odpovídá v polárních souřadnicích oblast N .
| > | s:=x=rho*cos(phi),y=rho*sin(phi); |
![]()
| > | i8u:=changevar({s},subs(M=N,i8),[rho,phi]); |
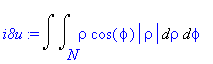
Nerovnice kruhu se transformuje v nerovnici
| > | subs(s,kruh); |
![]()
| > | simplify(%); |
![]()
Po vykrácení dostáváme
| > | rho<=2*r*cos(phi); |
![]()
Určíme meze pro integraci
| > | meze:=rho=0..rhs(%),phi=-Pi/2..Pi/2; |
![]()
Nakreslíme obrázek pro r=1
| > | plot(2*1*cos(phi),phi=-Pi/2..Pi/2,scaling=constrained); |
![[Maple Plot]](image/dvojnytrojny_komplet60.gif)
Počítáme tedy integrál
| > | assume(rho>0); |
| > | i8u:=Doubleint( integrand(i8u),meze); |
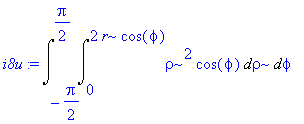
Postupnou integrací dostáváme
| > | value(%); |
![]()
| > |
| > |
Příklad 9
| > | restart:with(student):with(plots): |
Warning, the name changecoords has been redefined
Stanovme obsah kardioidy o rovnici
![]() . Kardioida je křivka patřící mezi epicykloidy, kdy pevná i kotálející se kružnice mají stejný poloměr.
. Kardioida je křivka patřící mezi epicykloidy, kdy pevná i kotálející se kružnice mají stejný poloměr.
Počítáme integrál
| > | i9:=Doubleint(1,x,y,M); |
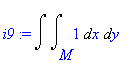
Nakreslíme obrázek pro a=1
| > | polarplot(1+cos(phi),phi=0..2*Pi); |
![[Maple Plot]](image/dvojnytrojny_komplet65.gif)
Zavedeme substituci do polárních souřadnic
| > | s:=x=rho*cos(phi),y=rho*sin(phi); |
![]()
| > | i9u:=changevar({s},subs(M=N,i9),[rho,phi]); # oblasti M zadané v kartézských souřadnicích odpovídá # v polárních souřadnicích oblast N |
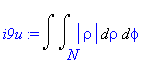
Integrační meze jsou
| > | meze:=rho=0..a*(1+cos(phi)),phi=0..2*Pi; |
![]()
Počítáme integrál
| > | i9u:=Doubleint(integrand(i9u),meze); |
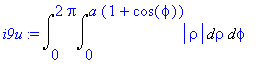
Postupnou integrací dostaneme
| > | assume(a>0); |
| > | value(%); |
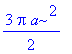
| > |
Objem tělesa
Nechť
g(x,y)
,
h(x,y)
jsou spojité funkce na oblasti
M
a platí
![]() uvnitř obrazce
M
. Označme
uvnitř obrazce
M
. Označme
![]() . Pak
T
je těleso a jeho objem definujeme
. Pak
T
je těleso a jeho objem definujeme
![]() .
.
Příklad 10
| > | restart:with(plots):with(student): |
Warning, the name changecoords has been redefined
Určete objem koule
T
, určené nerovností
![]() . Z rovnice kulové plochy
. Z rovnice kulové plochy
![]() vypočítáme
vypočítáme
![]() a volíme
a volíme
| > | g:=-sqrt(r^2-x^2-y^2): h:=sqrt(r^2-x^2-y^2): |
Obě funkce jsou definovány na kruhu
M
:
![]() , který získáme také kolmým průmětem do roviny
xy
. Dosazením do vzorce pro výpočet objemu dostáváme
, který získáme také kolmým průmětem do roviny
xy
. Dosazením do vzorce pro výpočet objemu dostáváme
| > | i10:=Doubleint((h-g),x,y,M); |
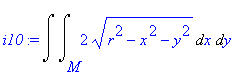
Po transformaci do polárních souřadnic dostáváme
| > | s:=x=rho*cos(phi),y=rho*sin(phi); |
![]()
| > | i10u:=changevar({s},subs(M=N,i10),[rho,phi]); |
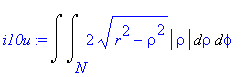
kde N je oblast v polárních souřadnicích ( odpovídá oblasti M zadané v kartézských souřadnicích ). Nové meze po transformaci
| > | meze:=rho=0..r,phi=0..2*Pi; |
![]()
Počítáme tedy integrál
| > | Doubleint(integrand(i10u),meze); |
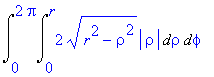
Postupnou integrací dostaneme
| > | assume(rho>0): |
| > | value(%); |
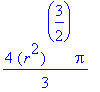
| > | assume(r>0): |
| > | simplify(%); |
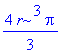
| > |
Příklad 11
| > | restart:with(plots):with(student): |
Warning, the name changecoords has been redefined
Určete objem tělesa ohraničeného rovinami
![]() .
.
Nejprve nakresleme obrázek
| > | implicitplot3d({x+y+z-1,x=0,y=0,z=0},x=-1..2,y=-1..2,z=-1..2); |
![[Maple Plot]](image/dvojnytrojny_komplet86.gif)
Průmětem tělesa do roviny
xy
je trojúhelník
M
ohraničený přímkami
![]() . Těleso je zdola ohraničeno rovinnou
xy
, proto
. Těleso je zdola ohraničeno rovinnou
xy
, proto
| > | g:=0; |
![]()
horní plochu tvoří rovina
| > | h:=1-x-y; |
![]()
Dosazením do vzorce pro výpočet objemu dostaneme
| > | i11:=Doubleint(h-g,y=0..1-x,x=0..1); |
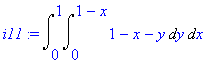
Postupnou integrací dostáváme
| > | i11=value(%); |
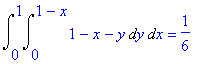
| > |
| > |
Příklad 12
| > | restart:with(plots):with(student): |
Warning, the name changecoords has been redefined
Vypočtěme objem tělesa, jehož hranici tvoří souřadnicové roviny a rovina
![]() .
.
Nakresleme obrázek pro
![]()
| > | implicitplot3d({x/2+y/2+z/2-1,x=0,y=0,z=0},x=-1..2,y=-1..2,z=-1..2); |
![[Maple Plot]](image/dvojnytrojny_komplet94.gif)
Průmětem tělesa je v rovině
xy
trojúhelník
![]() . Dolní plochou je
. Dolní plochou je
| > | g:=0; |
![]()
Horní plochou je
| > | h:=c*(1-x/a-y/b); |
![]()
Dosazením do vzorce pro výpočet objemu dostáváme
| > | i12:=Doubleint(h-g,y=0..b*(1-x/a),x=0..a); |
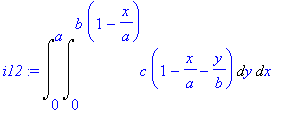
Integrací dostáváme
| > | i12=value(%); |
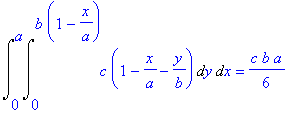
| > |
| > |
Příklad 13
| > | restart:with(plots):with(student): |
Warning, the name changecoords has been redefined
Stanovme objem tělesa ohraničeného souřadnicovými rovinami, rovinou
![]() a parabolickým válcem
a parabolickým válcem
![]() . Dále platí
. Dále platí
![]() .
.
Nakresleme obrázek pro
![]()
| > | implicitplot3d({x/2+y/2-1,x=0,y=0,z=0,z+x^2-4},x=0..2,y=0..2,z=-1..4, axes=boxed); |
![[Maple Plot]](image/dvojnytrojny_komplet104.gif)
Průmětem tělesa do roviny
xy
je trojúhelník
![[Maple OLE 2.0 Object]](image/dvojnytrojny_komplet105.gif) . Dolní plochou je rovina xy a horní plochou je parabolická plocha válce.
. Dolní plochou je rovina xy a horní plochou je parabolická plocha válce.
| > | g:=0; |
![]()
| > | h:=c^2-x^2; |
![]()
Dosazením do vzorce pro výpočet objemu dostáváme
| > | Doubleint(h-g,y=0..b*(1-x/a),x=0..a); |
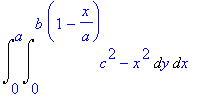
Integrací dostáváme
| > | value(%); |
![]()
| > |
První momenty obrazce M vzhledem k ose
-
x
:
![[Maple OLE 2.0 Object]](image/dvojnytrojny_komplet110.gif)
-
y
:
![[Maple OLE 2.0 Object]](image/dvojnytrojny_komplet111.gif)
Těžiště obrazce
![]()
![]()
Kvadratické momenty obrazce M vzhledem k osám x , y , z definujeme
![]() ,
,
![]() ,
,
![]()
Vzdálenost od osy z v naše případě znamená vzdálenost od počátku.
| > |
Příklad 14
| > | restart:with(plots):with(student): |
Warning, the name changecoords has been redefined
Určete první moment obdélníka o stranách a , b vzhledem k přímce, na které leží strana a . Umístíme ho do souřadnicového systému, jeho hranici tedy tvoří přímky o rovnicích.
| > | rce:=x=0,x=a,y=0,y=b; |
![]()
Nakreslíme obrázek pro a=2 , b=1
| > | implicitplot({x,x-2,y,y-1},x=0..3,y=0..2,thickness=2); |
![[Maple Plot]](image/dvojnytrojny_komplet118.gif)
Protože strana a leží na ose x , počítáme
| > | U[x](M):=Doubleint(y,x,y,M); |
 := Int(Int(y,x = M .. ``),y = `` .. ``)](image/dvojnytrojny_komplet119.gif)
Dosadíme hranice oblasti M do integrálu
| > | Doubleint(y,x=0..a,y=0..b); |
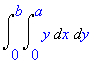
Spočítáme integrál
| > | value(%); |
![]()
Tento jednoduchý příklad slouží k odvození rozměru prvního momentu. V analytické geometrii rozměry neuvažujeme a můžeme použít i rovnice, které nejsou rozměrově správné. Vypočtené integrály však znamenají pouze hodnoty prvních momentů, které mají vždy rozměr
![]() , odpovídá-li jednotce 1 m.
, odpovídá-li jednotce 1 m.
| > |
| > |
Příklad 15
| > | restart:with(plots):with(student): |
Warning, the name changecoords has been redefined
Určeme souřadnice těžiště homogenního obrazce
M
, který je dán podmínkami
![]() .
.
Nejdříve si obrazec nakresleme pro r1=1 , r2=2 .
| > | implicitplot({2*1*x-x^2-y^2,x^2+y^2-2*2*x},x=0..4,y=-2..2); |
![[Maple Plot]](image/dvojnytrojny_komplet124.gif)
Z obrázku je patrné, že
![]() . Pro určení druhé souřadnice těžiště musíme spočítat obsah
. Pro určení druhé souřadnice těžiště musíme spočítat obsah
| > | P:=Doubleint(1,x,y,M); |
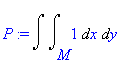
a první moment
| > | My:=Doubleint(x,x,y,M); |
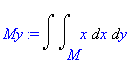
Zavedeme polární souřadnice
| > | s:=x=rho*cos(phi),y=rho*sin(phi); |
![]()
| > | P:=changevar({s},subs(M=N,P),[rho,phi]); |
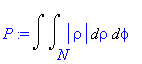
| > | My:=changevar({s},subs(M=N,My),[rho,phi]); |
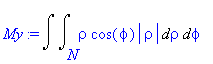
Obrazec M se zobrazí na obrazec N , pro který platí
| > | meze:=rho=2*r1*cos(phi)..2*r2*cos(phi),phi=-Pi/2..Pi/2; |
![]()
Dosazením dostaneme
| > | P:=Doubleint(integrand(P),meze); |
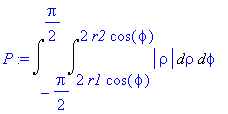
| > | My:=Doubleint(integrand(My),meze); |
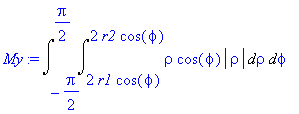
Spočteme hodnoty integrálů
| > | assume(rho>0); |
| > | P:=value(P); |
![]()
| > | My:=value(My); |
![]()
Dosazením do vzorce pro výpočet těžiště dostaneme
| > | x[T]:=simplify(My/P); |
![x[T] := (r1^2+r1*r2+r2^2)/(r1+r2)](image/dvojnytrojny_komplet136.gif)
| > |
| > |
Příklad 16
| > | restart:with(plots):with(student): |
Warning, the name changecoords has been redefined
Určete těžiště obrazce
M
ohraničeného křivkami
![]() .
.
Nakresleme obrázek
| > | plot([0,1-x^2],x=-2..2,y=-1..1,scaling=constrained,thickness=2); |
![[Maple Plot]](image/dvojnytrojny_komplet138.gif)
Spočteme obsah obrazce. Počítáme tedy integrál
| > | P:=Int(1-x^2,x=-1..1); |
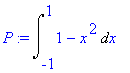
| > | P:=value(%); |
![]()
Dále spočteme první momenty. Jde o integrály
| > | Ux:=Doubleint(y,x,y,M); |
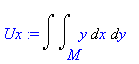
| > | Uy:=Doubleint(x,x,y,M); |
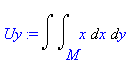
Dosadíme meze integrace
| > | Ux:=Doubleint(y,y=0..1-x^2,x=-1..1); |
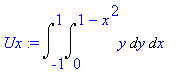
| > | Ux:=value(%); |
![]()
| > | Uy:=Doubleint(x,x=-sqrt(1-y)..sqrt(1-y),y=0..1); |
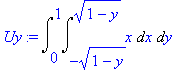
| > | Uy:=value(%); |
![]()
Dosazením do vzorců pro výpočet těžiště dostáváme
| > | x[T]:=Uy/P; |
![]()
| > | y[T]:=Ux/P; |
![]()
| > |
| > |
Příklad 17
| > | restart:with(plots):with(student): |
Warning, the name changecoords has been redefined
Určete kvadratický moment kruhu vzhledem k přímce procházející bodem na obvodu kolmo k rovině kruhu. Za střed
S
kruhu o poloměru
r
a zvolme bod
(r,0)
. Hranicí kruhu
M
je kružnice
![]() . Hledaný kvadratický moment je
. Hledaný kvadratický moment je
![]() .
.
Nakreslíme obrázek pro r=1
| > | rce:=(x-r)^2+y^2=r^2; |
![]()
| > | implicitplot((x-1)^2+y^2-1,x=0..2,y=-1..1); |
![[Maple Plot]](image/dvojnytrojny_komplet152.gif)
Výpočet provedeme transformací do polárních souřadnic
| > | s:=x=rho*cos(phi),y=rho*sin(phi); |
![]()
Transformací kružnice dostaneme
| > | subs({s},rce); |
![]()
| > | simplify(%); |
![]()
Vyřešíme rovnici vzhledem k
![]()
| > | solve(%,rho); |
![]()
Protože
![]() , plyne z nerovnosti
, plyne z nerovnosti
![]() omezení
omezení
![]() .
.
| > | meze:=rho=0..2*r*cos(phi),phi=-Pi/2..Pi/2; |
![]()
Dosazením do integrálu
| > | Ix:=Doubleint((x^2+y^2),x,y,M); |
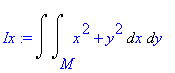
dostaneme integrál
| > | Ixu:=changevar({s},subs(M=N,Ix),[rho,phi]); |
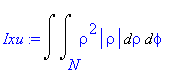
Obrazec N v polárních souřadnicích odpovídá obrazci M v kartézských.
Nakreslíme obrázek pro r=2
| > | plot(2*2*cos(phi),phi=-Pi/2..Pi/2); |
![[Maple Plot]](image/dvojnytrojny_komplet164.gif)
Dosazením mezí dostaneme
| > | Ixu:=Doubleint(integrand(Ixu),meze); |
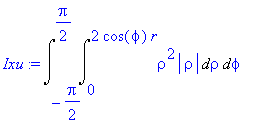
Integrací spočteme hodnotu kvadratického momentu
| > | assume(rho>0,r>0); map(value,%); |
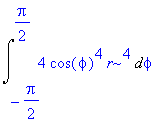
| > | value(%); |

Jednotkou kvadratického momentu je
![]() .
.
| > |
![[Maple Plot]](image/dvojnytrojny_komplet171.gif)
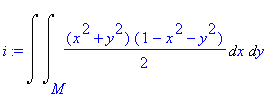
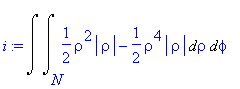
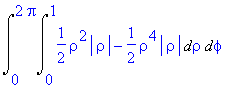
![[Maple Plot]](image/dvojnytrojny_komplet190.gif)
![[Maple OLE 2.0 Object]](image/dvojnytrojny_komplet202.gif)
![[Maple Plot]](image/dvojnytrojny_komplet207.gif)
![[Maple Plot]](image/dvojnytrojny_komplet212.gif)
![[Maple Plot]](image/dvojnytrojny_komplet231.gif)
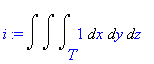
![[Maple OLE 2.0 Object]](image/dvojnytrojny_komplet238.gif)
![[Maple Plot]](image/dvojnytrojny_komplet242.gif)
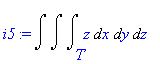
![[Maple OLE 2.0 Object]](image/dvojnytrojny_komplet253.gif) , kde
T
je koule
, kde
T
je koule
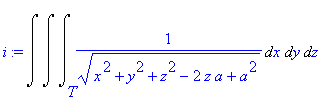
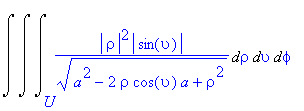
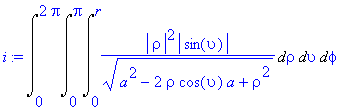
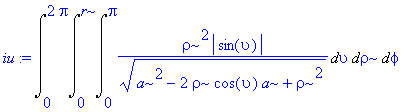
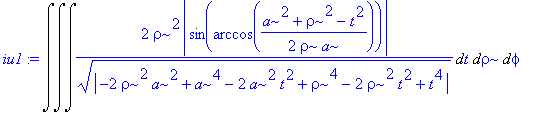
![[Maple OLE 2.0 Object]](image/dvojnytrojny_komplet268.gif)
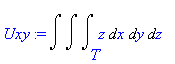
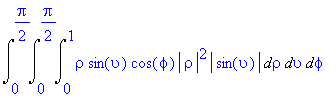
![[Maple Plot]](image/dvojnytrojny_komplet291.gif)
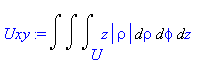
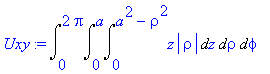
![z[T] := 1/3*a^2](image/dvojnytrojny_komplet304.gif)
![[Maple Plot]](image/dvojnytrojny_komplet307.gif)
![[Maple Plot]](image/dvojnytrojny_komplet312.gif)