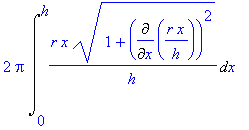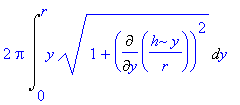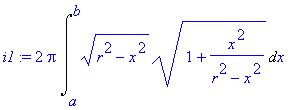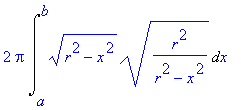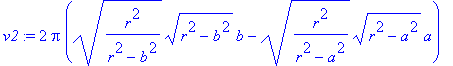Obsah rovinných obrazců
Nechť
g(x)
a
h(x)
jsou funkce spojité na intervalu
![]() a platí
a platí
![]() na
na
![]() . Označme
. Označme
![]() . Pak obsah obrazce
M
je roven
. Pak obsah obrazce
M
je roven
![]() .
.
Poznámky:
-
Je-li funkce
h(x)
dána parametrickými rovnicemi
![[Maple OLE 2.0 Object]](image/aplikace_komplet6.gif) , které jsou spojité a platí
, které jsou spojité a platí
![[Maple OLE 2.0 Object]](image/aplikace_komplet7.gif) a funkce
g(x) = 0
. Pak substitucí
a funkce
g(x) = 0
. Pak substitucí
![[Maple OLE 2.0 Object]](image/aplikace_komplet8.gif) dostáváme
dostáváme
![[Maple OLE 2.0 Object]](image/aplikace_komplet9.gif)
-
Je-li obrazec
M
zadán v polárních souřadnicích nerovnicemi
![[Maple OLE 2.0 Object]](image/aplikace_komplet10.gif) , kde
, kde
![[Maple OLE 2.0 Object]](image/aplikace_komplet11.gif) je spojitá na
je spojitá na
![[Maple OLE 2.0 Object]](image/aplikace_komplet12.gif) , pak jeho obsah určíme vzorcem
, pak jeho obsah určíme vzorcem
![[Maple OLE 2.0 Object]](image/aplikace_komplet13.gif) .
.
V této části budeme používat příkazy pro vykreslování grafů funkcí, proto je vhodné nejdříve prostudovat kapitolu Základy grafického zpracování .
| > |
Příklad 1
Určeme obsah obrazce, který je ohraničen parabolami.
| > | restart:with(plots):with(student): |
Warning, the name changecoords has been redefined
Paraboly jsou zadány rovnicemi
| > | p1:=3*y=x^2-2; p2:=y=x^2-4/3*x-6; |
![]()
![]()
Vykreslíme graf funkcí
| > | implicitplot({p1,p2},x=-4..5,y=-7..6); |
![[Maple Plot]](image/aplikace_komplet16.gif)
Určíme průsečíky obou parabol
| > | intercept(p1,p2); |
![]()
Vyjádříme y z obou rovnic
| > | h:=isolate(p1,y); |
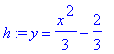
| > | g:=isolate(p2,y); |
![]()
Vytvoříme argument pro dosazení do vzorce
| > | F:=unapply(rhs(h-g),x); |
![]()
Počítáme tedy integrál
| > | i1:=Int(F(x),x=-2..4); |
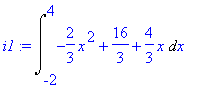
Obsah tedy je
| > | value(%); |
![]()
| > |
Příklad 2
Určete obsah obrazce, který je ohraničen osou y a semikubickou parabolou.
| > | restart:with(plots):with(student): |
Warning, the name changecoords has been redefined
Rovnice semikubické paraboly
| > | p:=[y^2=(a-x)^3]; |
![]()
| > | #assume(a>0); |
Pokus o vykreslení funkce dané implicitně. Je vidět, že systém Maple má určité problémy. Pro nakreslení grafu je samozřejmě nutné zvolit pevné a .
| > | implicitplot(y^2=(2-x)^3,x=0..3,y=-10..10); |
![[Maple Plot]](image/aplikace_komplet24.gif)
Rozdělíme předepsanou funkci na dvě
| > | h:=sqrt((a-x)^3); |
![]()
| > | g:=-sqrt((a-x)^3); |
![]()
Vykreslíme graf funkcí h , g pro pevně zvolené a=10 .
| > | p1:=plot(sqrt((10-x)^3),x=-2..10): |
| > | p2:=plot(-sqrt((10-x)^3),x=-2..10): |
| > | display({p1,p2}); |
![[Maple Plot]](image/aplikace_komplet27.gif)
Určíme průsečík s osou x , tj. y=0 . Příkaz intercept spočítá průsečík dvou křivek.
| > | intercept(h=0,y=0); |
![]()
Počítáme tedy integrál
| > | i2:=Int(h-g,x=0..a); |
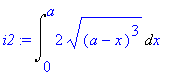
Výsledný obsah
| > | value(i2); |
![]()
| > |
Příklad 3
Určete obsah obrazce ohraničeného obloukem cykloidy a osou x .
| > | restart:with(plots):with(student): |
Warning, the name changecoords has been redefined
Rovnice cykloidy
| > | rce:=[r*(t-sin(t)),r*(1-cos(t))]; #assume(0<=t,t<=2*Pi); |
![]()
Nakreslení grafu. Rovnice jsou děleny v argumentu r , abychom dostali konkrétní vyjádření.
| > | plot([rce[1]/r,rce[2]/r,t=0..2*Pi],scaling=constrained); |
![[Maple Plot]](image/aplikace_komplet32.gif)
Užijeme vzorce pro výpočet obsahu obrazce ohraničeným funkcemi danými parametricky
| > | P(M)=Int(psi(t)*D(phi(t)),t=alpha..beta); |
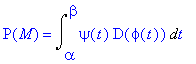
Dosazením dostáváme
| > | i3:=Int(rce[2]*diff(rce[1],t),t=0..2*Pi); |
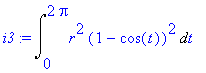
Spočteme obsah
| > | value(i3); |
![]()
| > |
| > |
Příklad 4
Určete obsah obrazce 1.kvadrantu ohraničeného Archimedovou spirálou a přímkami
| > | restart:with(plots):with(student): |
Warning, the name changecoords has been redefined
Omezení na plochu
| > | p:=rho=a*phi; # archimedova spirála phi=Pi/3; # přímka phi=Pi/2; # přímka |
![]()
![]()
![]()
Vykreslení plochy
| > | pl1:=polarplot(phi,phi=0..4/3*Pi): |
| > | pl2:=plot(Pi/3*x,x=0..1): |
| > | display({pl1,pl2}); |
![[Maple Plot]](image/aplikace_komplet39.gif)
Dosadíme-li do odpovídajícího intergrálu dostaneme
| > | i4:=1/2*Int(a^2*phi^2,phi=Pi/3..Pi/2); |
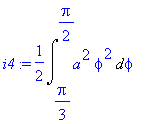
Výsledná plocha je
| > | value(%); |
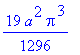
| > |
![[Maple OLE 2.0 Object]](image/aplikace_komplet45.gif) v případě, kdy prostorová křivka
C
je zadána parametrickými rovnicemi
v případě, kdy prostorová křivka
C
je zadána parametrickými rovnicemi
![[Maple OLE 2.0 Object]](image/aplikace_komplet51.gif) v případě, kdy rovinná křivka
C
je zadána rovnicí
v případě, kdy rovinná křivka
C
je zadána rovnicí
![[Maple Plot]](image/aplikace_komplet55.gif)
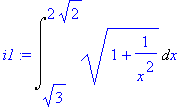
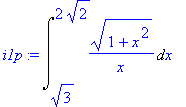
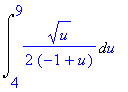
![[Maple Plot]](image/aplikace_komplet63.gif)
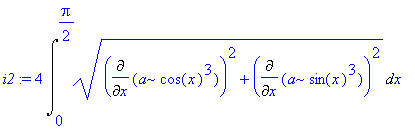
![[Maple Plot]](image/aplikace_komplet67.gif)
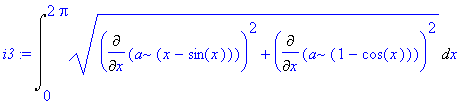
![[Maple Plot]](image/aplikace_komplet72.gif)
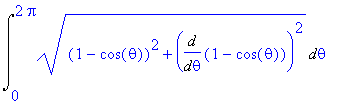
![[Maple Plot]](image/aplikace_komplet76.gif)
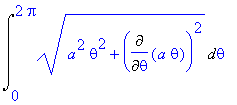
![[Maple OLE 2.0 Object]](image/aplikace_komplet84.gif) v případě, kdy těleso V vzniká rotací rovinné oblasti
v případě, kdy těleso V vzniká rotací rovinné oblasti
![[Maple Plot]](image/aplikace_komplet92.gif)
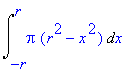
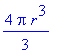
![[Maple Plot]](image/aplikace_komplet96.gif)
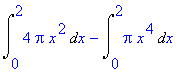
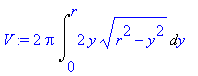
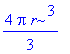
![[Maple Plot]](image/aplikace_komplet107.gif)
![[Maple Plot]](image/aplikace_komplet108.gif)
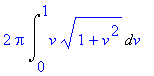
![[Maple OLE 2.0 Object]](image/aplikace_komplet117.gif) v případě, kdy plocha
S
vzniká rotací grafu
v případě, kdy plocha
S
vzniká rotací grafu
![[Maple Plot]](image/aplikace_komplet122.gif)
![[Maple Plot]](image/aplikace_komplet123.gif)