Příklad 3

Určete tok polohového vektoru přes horní stranu úseku hyperbolického paraboloidu definovaného nad čtvercem  ležícím v souřadnicové rovině xy .

>	restart:with(plots):with(VectorCalculus):with(student):

Warning, the name changecoords has been redefined

Warning, the assigned names <,> and <|> now have a global binding

Warning, these protected names have been redefined and unprotected: *, +, ., Vector, diff, int, limit, series

>	Doubleint(x,y,z,S)+Doubleint(y,x,z,S) +Doubleint(z,x,y,S);

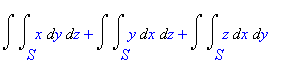
Úsek je silně regulární vzhledem k rovině xy , proto můžeme použít postup z předchozího příkladu. Užijeme tedy následujícího vyjádření .

Rovnice hyperbolického paraboloidu

>	par:=z=x*y+a^2;

Nakreslíme obrázek pro a=1 .

>	p:=fieldplot3d([x,y,z],x=-1..3,y=-1..3,z=-1..3, grid=[5,5,5],color=red):

>	p1:=implicitplot3d(subs(a=1,par),x=0..2,y=0..2, z=0..3,axes=normal,orientation=[-60,70]):

#  Parametr axes  určuje zobrazení souřadnicové soustavy.

>	display({p,p1});

Určíme normálu

>	n:=[-diff(rhs(par),x),-diff(rhs(par),y),1];

Podle z -ové složky určíme

>	epsilon[z]=1;

Zápis integrandů

>	P:=x;Q:=y;R:=x*y+a^2;

Spočteme příslušný skalární součin

>	linalg[dotprod](n,[P,Q,R],'orthogonal');

Plocha je omezena čtvercem v rovině xy . Tedy počítáme integrál

>	Doubleint(%,x=0..a,y=0..a);

>

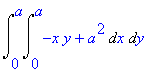
value(%);

Výpočet pomocí knihovny VectorCalculus

>	Flux(VectorField(<x,y,z>,'cartesian[x,y,z]'), Surface(<s,t,s*t+a^2>,s=0..a,t=0..a));

>