Příklad 2

Předchozí integrál spočtěme pomocí skalárního součinu.

V případě silné regularity k jedné ze souřadnicových rovin, je možné plošný integrál přepsat na integrál se skalárním součinem dvou vektorů. Pro silnou regularitu vzhledem k rovině xy  můžeme integrál zapsat     

kde f(x,y)  získáme vyjádřením proměnné z  ze zadané roviny.

>	restart:with(plots):with(VectorCalculus):with(student):

Warning, the name changecoords has been redefined

Warning, the assigned names <,> and <|> now have a global binding

Warning, these protected names have been redefined and unprotected: *, +, ., Vector, diff, int, limit, series

>	f:=isolate(x-y+z-1,z);

Zadání integrálu

>	P:=y; Q:=x; R:=1-x+y;

Rozsah proměnných x , y  získáme průmětem plochy do roviny xy .

>	rx:=x=0..1; ry:=y=x-1..0;

Spočteme požadované derivace

>	n:=[-diff(rhs(f),x),-diff(rhs(f),y),1];

Vzhledem k souhlasné orientaci této normály se zadanou normálou, položíme

>	epsilon[z]=1;

Spočteme skalární součin pomocí příkazu dotprod  z knihovny linalg .

>	v:=simplify(linalg[dotprod](n,[P,Q,R],'orthogonal'));

#  Parametr orthogonal  je uveden pro tradiční výpočet skalárního součinu.

Po dosazení počítáme následující integrál

>	Doubleint(v,ry,rx);

>

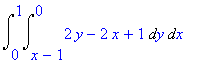
value(%);

>