Příklad 1

Vypočtěte plošný integrál přes danou plochu.

>	restart:with(plots):with(VectorCalculus):with(student):

Warning, the name changecoords has been redefined

Warning, the assigned names <,> and <|> now have a global binding

Warning, these protected names have been redefined and unprotected: *, +, ., Vector, diff, int, limit, series

>	Doubleint(y,y,z,S)+Doubleint(x,x,z,S)+Doubleint(z,x,y,S);

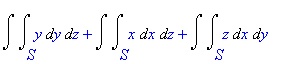
Určíme vektorové pole pomocí integrandů jednotlivých integrálů.

>	vpole:=[y,x,z];

Plocha je zadána pomocí trojúhelníka ležícího v rovině

>	rov1:=x-y+z=1;

který je vymezen rovinami

>	rov2:=x>=0,y<=0,z>=0;

Trojúhelník je orientován vektorem svírajícím ostrý úhel s kladnou poloosou z .

Nakreslíme obrázek

>	p1:=fieldplot3d(vpole,x=-2..2,y=-2..2,z=-2..2, color=red,thickness=2,grid=[5,5,5]):

#  Vektorové pole ve 3D

>	p2:=implicitplot3d(x>=0,x=-2..2,y=-2..2,z=-2..2, color=yellow):

>	p3:=implicitplot3d(y<=0,x=-2..2,y=-2..2,z=-2..2, color=yellow):

>	p4:=implicitplot3d(z>=0,x=-2..2,y=-2..2,z=-2..2, color=yellow):

>	p5:=implicitplot3d(x-y+z=1,x=-2..2,y=-2..2,z=-2..2, color=green):

#  Nakreslení daných rovin v implicitném tvaru.

>	display({p1,p2,p3,p4,p5},axes=boxed, orientation=[-60,45],style=patchnogrid);

#  Parametr patchnogrid  zakazuje vykreslení triangulace na zadané ploše

Nyní přistupme k výpočtu integrálu. Rozdělme výše uvedený integrál na tři dílčí. Výpočet ukážeme na jednom z nich, ostatní budou spočteny analogicky.
Počítejme tedy integrál

>	epsilon[x]*Doubleint(y,y,z,S[yz]);

Plocha je v tomto případě silně regulární vzhledem k rovině yz .
Z rovnice roviny vyjádříme proměnnou x .

>	h:=isolate(rov1,x);

Průmětem dané roviny do roviny yz  dostaneme trojúhelník a tím i meze pro integraci.

>	ry:=y=-1..0; rz:=z=0..y+1;

Pro lepší představu nakreslíme obrázek

>	implicitplot(y-z+1,y=-2..2,z=-2..2);

Dále určíme normálový vektor, který má tvar .

Spočteme požadované derivace

>	n:=[1,-diff(rhs(h),y),-diff(rhs(h),z)];

Protože normálový vektor svírá s kladnou poloosou z  ostrý úhel ( určeno pomocí třetí souřadnice normálového vektoru n ), má tato normála stejný směr jako je směr předepsané normály, proto klademe

>	epsilon[x]=1;

Počítáme tedy integrál

>	i1:=1*Doubleint(y,rz,ry);

>

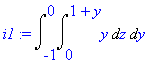
value(%);

Zbylé dva integrály spočteme analogicky

>	epsilon[y]*Doubleint(x,x,z,S[xz]); epsilon[z]*Doubleint(z,x,y,S[xy]);

Plocha je v tomto případě silně regulární vzhledem k rovině xz , popř. xy .
Z rovnice roviny vyjádříme proměnnou y , popř. z .

>	q:=isolate(rov1,y); f:=isolate(rov1,z);

Průmětem dané roviny do roviny xz  dostaneme trojúhelník a tím i meze pro integraci.

>	qx:=x=0..1; qz:=z=0..1-x;

Průmětem dané roviny do roviny xy  dostaneme trojúhelník a tím i meze pro integraci.

>	fx:=x=0..1; fy:=y=-1+x..0;

Normálové vektory jsou tvaru .

 Spočteme požadované derivace

>	nq:=[-diff(rhs(q),x),1,-diff(rhs(q),z)]; nf:=[-diff(rhs(f),x),-diff(rhs(f),y),1];

Protože normálový vektor svírá s kladnou poloosou z  tupý, resp. ostrý, úhel  ( určeno pomocí třetí souřadnice normálového vektoru n ), má normála opačný, resp.stejný směr, jako je směr předepsané normály, proto klademe

>	epsilon[y]=-1; epsilon[z]=1;

Počítáme tedy integrály

>	i2:=-1*Doubleint(x,qz,qx); i3:=1*Doubleint(rhs(f),fy,fx);

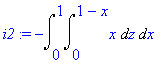
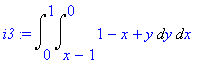
Výsledný integrál je dán součtem dílčích integrálů

>	value(i1+i2+i3);

Výpočet pomocí knihovny VectorCalculus

>	Flux(VectorField(<y,x,z>,'cartesian[x,y,z]'), Surface( <s,t,1-s+t>, s=0..1, t=-1+s..0));

#  Orientace normály je implicitně nastavena.  

>